2 偏微分
本章の目次
- 2.1
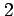 変数関数
変数関数
- 2.2 極限
- 2.3 連続性
- 2.4 多変数関数の微分
- 2.5 偏微分
- 2.6
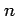 変数関数の偏微分
変数関数の偏微分
- 2.7 高階偏微分
- 2.8 ランダウの記号
- 2.9 1 変数関数の微分
- 2.10 全微分
- 2.11
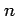 変数関数の全微分
変数関数の全微分
- 2.12 全微分と偏微分
- 2.13 全微分と連続
- 2.14 1 変数関数の合成関数の微分
- 2.15 2 変数関数 と 1 変数関数の合成関数の微分
- 2.16 2 変数関数 と 2 変数関数の合成関数の微分
- 2.17
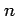 変数関数と 1 変数関数の合成関数の微分
変数関数と 1 変数関数の合成関数の微分
- 2.18
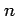 変数関数と
変数関数と 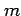 変数関数の合成関数の微分
変数関数の合成関数の微分
- 2.19 偏微分作用素
- 2.20 座標変換
- 2.21 斜交座標
- 2.22 2 次元空間の極座標
- 2.23 3 次元空間の極座標
- 2.24 調和関数
- 2.25 方向微分
- 2.26 ライプニッツ則
- 2.27 テイラー展開
- 2.28
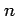 変数関数のテイラー展開
変数関数のテイラー展開
- 2.29 平均値の定理
- 2.30 1 変数の陰関数
- 2.31 接線
- 2.32 2 変数の陰関数
- 2.33 陰関数の高階導関数
- 2.34 接平面
- 2.35 極値
- 2.36 条件付き極値問題
Kondo Koichi

平成18年1月18日