2.13 全微分と連続
定理 2.61 (全微分可能と連続)
関数 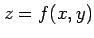 が全微分可能であれば,
が全微分可能であれば,
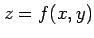 は連続関数である.
は連続関数である.
が成り立つ. このとき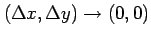 の極限をとる.
右辺は
の極限をとる.
右辺は
となる. よって左辺も 0 となるので,
を得る. 点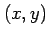 への
極限
への
極限
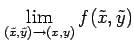 が存在し,かつ点
が存在し,かつ点 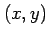 における値
における値  と等しいので,
関数
と等しいので,
関数  は任意の点
は任意の点 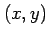 について連続である.
について連続である.
(証明)
関数 ![]() が全微分可能であれば,
が全微分可能であれば,
が成り立つ. このとき
となる. よって左辺も 0 となるので,
を得る. 点
Kondo Koichi

平成18年1月18日