1.5 演習問題 〜 直線,平面
| 2 点 |
||||||
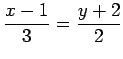 |
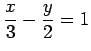 |
(1) 点 ![]() ,
, ![]() を通る直線
(2) 点
を通る直線
(2) 点 ![]() ,
, ![]() を通る直線
を通る直線
(3) 点 ![]() ,
, ![]() を通る直線
(4) 点
を通る直線
(4) 点 ![]() ,
, ![]() を通る直線
を通る直線
(5)
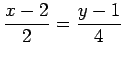 (6)
(6)
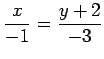 (7)
(7)
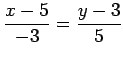 (8)
(8)
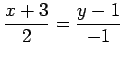
(9) ![]() (10)
(10) ![]() (11)
(11) ![]() (12)
(12) ![]()
(13) ![]() (14)
(14) ![]() (15)
(15) ![]()
(16) ![]() (17)
(17)
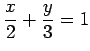 (18)
(18)
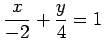
(19)
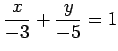 (20)
(20)
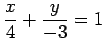
(1)
![]() (2) 3 点
(2) 3 点 ![]() ,
, ![]() ,
, ![]() を通る平面
を通る平面
(1) 点 ![]() ,
, ![]() ,
, ![]() (2) 点
(2) 点 ![]() ,
, ![]() ,
, ![]()
(3) 点 ![]() ,
, ![]() ,
, ![]() (4) 点
(4) 点 ![]() ,
, ![]() ,
, ![]()
(1) ![]() ,
, ![]() (2)
(2) ![]() ,
, ![]()
(3) 2 点 ![]() ,
, ![]() を通る直線
を通る直線
(1) 点 ![]() ,
, ![]() (2) 点
(2) 点 ![]() ,
, ![]() (3) 点
(3) 点 ![]() ,
, ![]()
(4) 点 ![]() ,
, ![]()
(1)
![]() ,
,
![]() (2)
(2)
![]() ,
,
![]()
(1) ![]() (2)
(2) ![]() (3)
(3) ![]() (4)
(4)
![]()
(1)
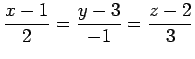 (2)
(2)
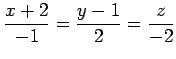
(1) ![]() ,
, ![]() ,
, ![]() ,
, ![]() (2)
(2) ![]() ,
, ![]() ,
, ![]() ,
, ![]()
(3) ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Kondo Koichi

平成18年1月18日