2.9 1 変数関数の微分
定義 2.47 (微分可能)
関数 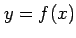 において,
点
において,
点  から 点
から 点
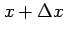 への増分
への増分
に対して
をみたす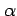 が存在するとき,
が存在するとき,
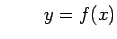 は微分可能であるという.
このとき
は微分可能であるという.
このとき
と表記し,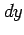 を
を 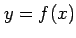 の微分という.
の微分という.
に対して
をみたす
と表記し,
定理 2.48 (微分)
関数 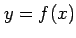 が微分可能であることの必用十分条件は,
極限
が微分可能であることの必用十分条件は,
極限
が存在することである. このとき
が成り立つ.
となる.このとき,
が成り立つ. よって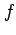 が微分可能であることと極限
が微分可能であることと極限 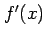 が存在することとは
必要十分条件であり,
が存在することとは
必要十分条件であり,
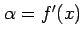 となる.
となる.
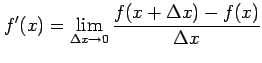 |
が存在することである. このとき
が成り立つ.
(証明)
![]() とおく.
ただし,
とおく.
ただし,
![]() であり,
であり,
![]() は
は
![]() についてのある関数とする.
についてのある関数とする.
![]() について式変形すると
について式変形すると
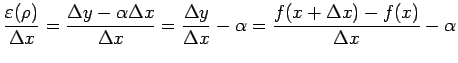 |
となる.このとき,
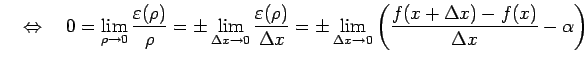 |
||
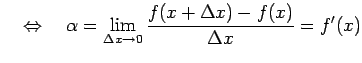 |
が成り立つ. よって
例 2.49 (微分可能)
関数
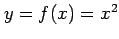 に関して
に関して
とおく. このとき
が成り立つ.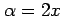 のとき 0 となるから,
のとき 0 となるから,
が成り立つ.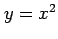 は微分可能であり,
は微分可能であり,
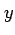 の微分は
の微分は
である.
とおく. このとき
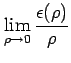 |
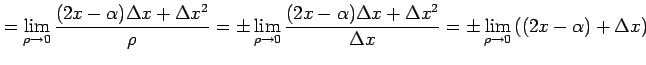 |
|
が成り立つ.
が成り立つ.
である.
Kondo Koichi

平成18年1月18日