2.25 方向微分
定義 2.107 (方向微分)
関数
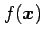 の点
の点 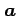 における方向
における方向 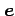 の
方向微分は
の
方向微分は
により定義される.
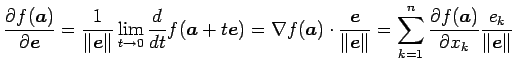 |
により定義される.
(証明) typing...
例 2.108 (方向微分)
関数
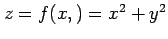 の点
の点 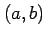 における
方向
における
方向
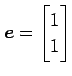 の微分は,
の微分は,
を用いて,
となる.
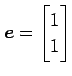 の微分は,
の微分は,
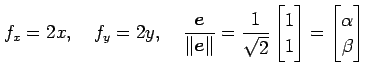 |
を用いて,
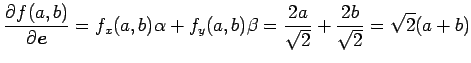 |
となる.
Kondo Koichi

平成18年1月18日