2.36 条件付き極値問題
定理 2.160 (ラグランジュの未定乗数法)
条件 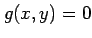 のもとでの関数
のもとでの関数 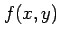 の極値の候補は,
の極値の候補は,
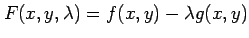 とおき,
とおき,
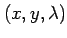 についての連立方程式
についての連立方程式
を解くことで得られる. これを ラグランジュの未定乗数法(Lagrange multiplier method) という.
とみなされる. ここで, 関数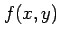 が点
が点 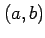 で極値をもつとする.
このとき
で極値をもつとする.
このとき 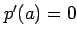 ,
, 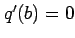 となるので,
となるので,
が成り立つ.また,
を用いると 2 つの式は
と 1 つの式となる. この方程式を解くことで極値の候補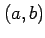 が定まる.
しかし,この方程式のままでは解くのが難しい.
次のように式変形する.
(☆)を変形して
が定まる.
しかし,この方程式のままでは解くのが難しい.
次のように式変形する.
(☆)を変形して
とおく.これを(☆)へ代入して
を得る. ここで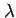 も未知変数であると考えて,
条件
も未知変数であると考えて,
条件 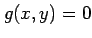 とあわせて,
とあわせて,
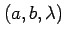 についての連立方程式とみなす.
についての連立方程式とみなす.
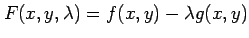 とおけば,
この 3 つの方程式は
とおけば,
この 3 つの方程式は
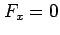 ,
, 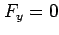 ,
,
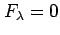 と表される.
と表される.
を解くことで得られる. これを ラグランジュの未定乗数法(Lagrange multiplier method) という.
(証明)
条件 ![]() より
より ![]() と
と ![]() は独立ではないから,
陰関数
は独立ではないから,
陰関数
![]() ,
, ![]() が存在する.
このとき,関数
が存在する.
このとき,関数 ![]() は 1 変数関数
は 1 変数関数
とみなされる. ここで, 関数
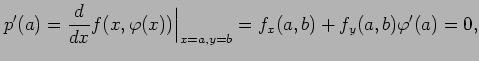 |
||
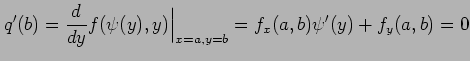 |
が成り立つ.また,
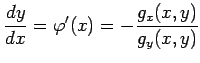 (ただし, (ただし, |
||
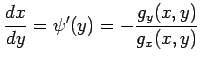 (ただし, (ただし, |
を用いると 2 つの式は
と 1 つの式となる. この方程式を解くことで極値の候補
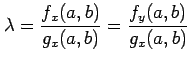 |
とおく.これを(☆)へ代入して
を得る. ここで
例 2.161 (条件付き極値)
条件
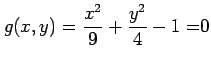 のもとでの
関数
のもとでの
関数
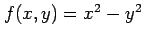 の
極値を求める.
まず,
の
極値を求める.
まず,
とおく.このとき連立方程式
を考える.これをまとめると
となる.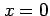 のとき第 3 式より
のとき第 3 式より 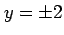 であり,
第 2 式より
であり,
第 2 式より
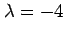 となる.
となる.
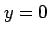 のとき第 3 式より
のとき第 3 式より 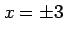 であり,
第 1 式より
であり,
第 1 式より 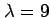 となる.
となる.
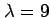 のとき
第 2 式より
のとき
第 2 式より 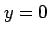 であり,
第 3 式より
であり,
第 3 式より 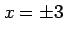 となる.
となる.
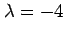 のとき
第 1 式より
のとき
第 1 式より 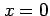 であり,
第 3 式より
であり,
第 3 式より 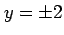 となる.
よって連立方程式の解は
となる.
よって連立方程式の解は
となる.極値の候補となる点は
である. これらの点が極値であるか確認する. 条件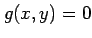 により定まる 2 つの
陰関数をそれぞれ
により定まる 2 つの
陰関数をそれぞれ
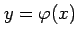 ,
, 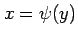 とおく.
これらの導関数は
とおく.
これらの導関数は
となる. また,合成関数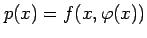 ,
,
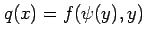 の
導関数はそれぞれ
の
導関数はそれぞれ
となる.さらに微分すると
となる. よって,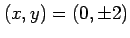 のとき,
のとき,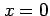 となるから
となるから 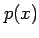 を用いて
を用いて
となるので,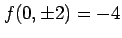 は極小値である.
また,
は極小値である.
また,
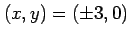 のとき,
のとき,
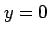 となるから
となるから 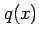 を用いて
を用いて
となるので,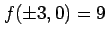 は極大値である.
は極大値である.
![\includegraphics[width=0.9\textwidth]{joken-kyokuchi.eps}](img1241.png)
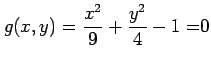 のもとでの
関数
のもとでの
関数
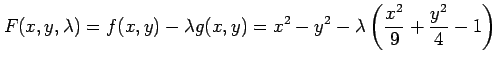 |
とおく.このとき連立方程式
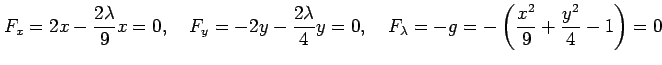 |
を考える.これをまとめると
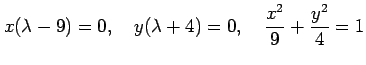 |
となる.
となる.極値の候補となる点は
である. これらの点が極値であるか確認する. 条件
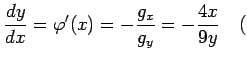 ただし ただし |
||
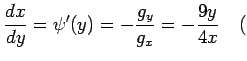 ただし ただし |
となる. また,合成関数
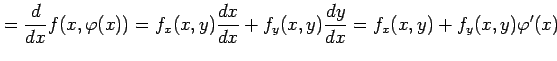 |
||
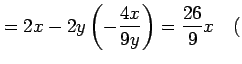 ただし ただし |
||
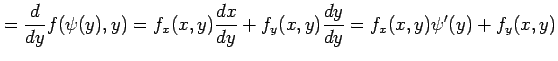 |
||
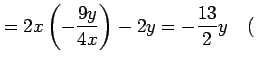 ただし ただし |
となる.さらに微分すると
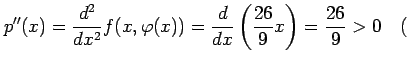 ただし ただし |
||
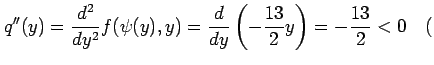 ただし ただし |
となる. よって,
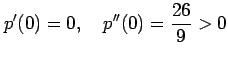 |
となるので,
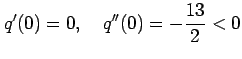 |
となるので,
![\includegraphics[width=0.9\textwidth]{joken-kyokuchi.eps}](img1241.png)
例 2.162 (条件付き極値)
条件
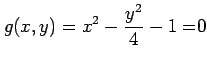 のもとでの
関数
のもとでの
関数
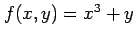 の極値を求める.
まず,
の極値を求める.
まず,
とおく.このとき連立方程式
を考える.これをまとめると
となる. 第 1 式より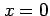 とする.
このとき第 3 式より
とする.
このとき第 3 式より
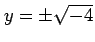 となり
実数解をもたないので不適である.
第 1 式より
となり
実数解をもたないので不適である.
第 1 式より
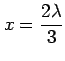 とする.
このとき,
とする.
このとき,
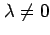 である.
なぜなら,
である.
なぜなら,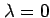 とすると
とすると 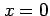 となるからである.
よって第 2 式より
となるからである.
よって第 2 式より
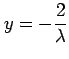 である.
である.
を第 3 式に代入すると
となる.実数の範囲内の解は
である. 以上より,連立方程式の解は
となる.極値の候補となる点は
である. これらの点が極値であるか確認する. 条件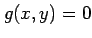 により定まる陰関数を
により定まる陰関数を
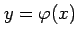 とおく.
この導関数は
とおく.
この導関数は
となる. また,合成関数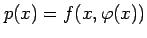 の導関数は
の導関数は 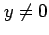 のとき
のとき
となる.さらに微分すると
となる. よって,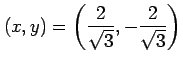 のとき,
のとき,
となるので,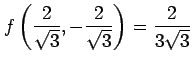 は極小値であり,
は極小値であり,
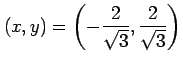 のとき,
のとき,
となるので,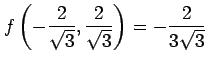 は極大値である.
は極大値である.
![\includegraphics[width=0.9\textwidth]{joken-kyokuchi2.eps}](img1268.png)
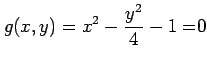 のもとでの
関数
のもとでの
関数
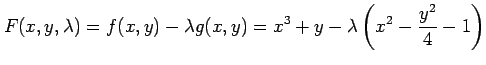 |
とおく.このとき連立方程式
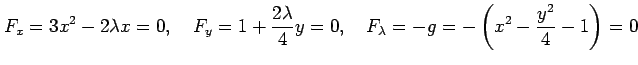 |
を考える.これをまとめると
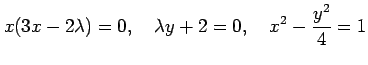 |
となる. 第 1 式より
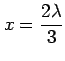 とする.
このとき,
とする.
このとき,
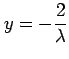 である.
である.
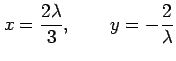 |
を第 3 式に代入すると
となる.実数の範囲内の解は
である. 以上より,連立方程式の解は
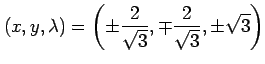 (複合同順) (複合同順) |
となる.極値の候補となる点は
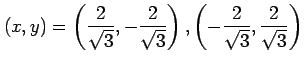 |
である. これらの点が極値であるか確認する. 条件
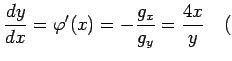 ただし ただし |
となる. また,合成関数
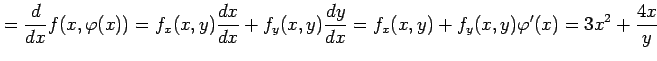 |
となる.さらに微分すると
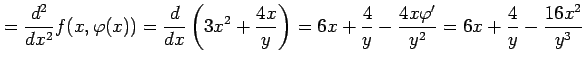 |
||
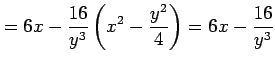 |
となる. よって,
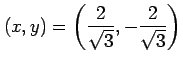 のとき,
のとき,
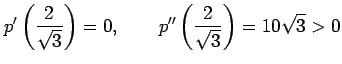 |
となるので,
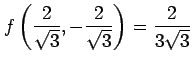 は極小値であり,
は極小値であり,
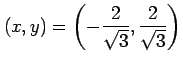 のとき,
のとき,
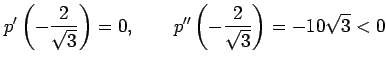 |
となるので,
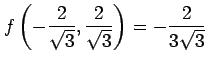 は極大値である.
は極大値である.
![\includegraphics[width=0.9\textwidth]{joken-kyokuchi2.eps}](img1268.png)
例 2.163 (条件付き極値)
条件
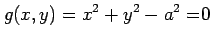 (
(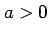 ) のもとでの
関数
) のもとでの
関数
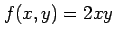 の極値を求める.
まず,
の極値を求める.
まず,
とおく.このとき連立方程式
を考える.これをまとめると
となる. 第 1 式より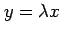 を第 2 式に代入して
を第 2 式に代入して
となる.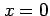 のとき,第 1 式では
のとき,第 1 式では 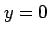 となり,
第 3 式では
となり,
第 3 式では 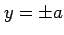 となる.
これは矛盾するので不適である.
となる.
これは矛盾するので不適である.
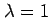 のとき,
のとき,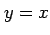 であり
第 3 式から
であり
第 3 式から
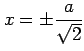 となる.
となる.
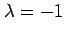 のとき,
のとき,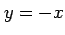 であり
第 3 式から
であり
第 3 式から
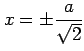 となる.
以上より,連立方程式の解は
となる.
以上より,連立方程式の解は
となる.極値の候補となる点は
である. これらの点が極値であるか確認する. 条件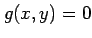 により定まる陰関数を
により定まる陰関数を
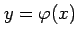 とおく.
この導関数は
とおく.
この導関数は
となる. また,合成関数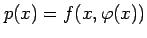 の導関数は
の導関数は 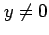 のとき
のとき
となる.さらに微分すると
となる. よって,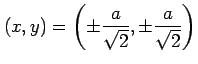 のとき,
のとき,
となるので,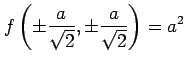 は極大値である.
は極大値である.
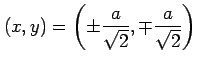 のとき,
のとき,
となるので,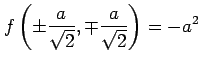 は極小値である.
は極小値である.
とおく.このとき連立方程式
を考える.これをまとめると
となる. 第 1 式より
となる.
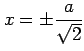 となる.
となる.
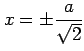 となる.
以上より,連立方程式の解は
となる.
以上より,連立方程式の解は
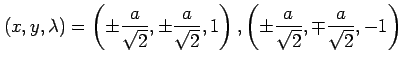 (複合同順) (複合同順) |
となる.極値の候補となる点は
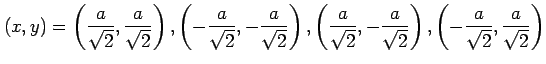 |
である. これらの点が極値であるか確認する. 条件
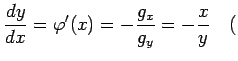 ただし ただし |
となる. また,合成関数
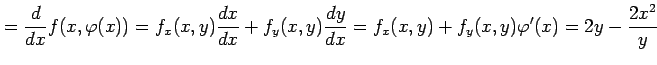 |
となる.さらに微分すると
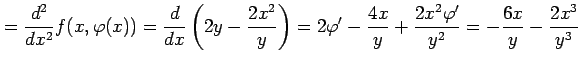 |
となる. よって,
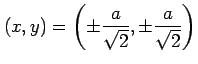 のとき,
のとき,
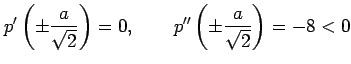 |
となるので,
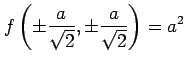 は極大値である.
は極大値である.
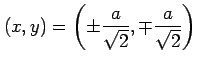 のとき,
のとき,
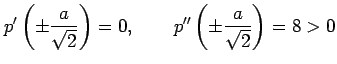 |
となるので,
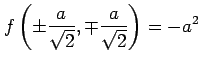 は極小値である.
は極小値である.
Kondo Koichi

平成18年1月18日