2.21 斜交座標
![]() 次元ユークリッド空間に
普通に導入する座標
次元ユークリッド空間に
普通に導入する座標 ![]() は,
標準基底
は,
標準基底
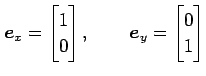 |
における座標である. 座標を
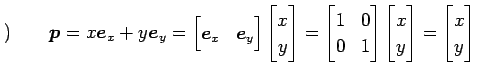 |
と表される. 一方, 基底
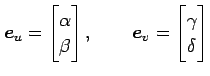 |
における座標を
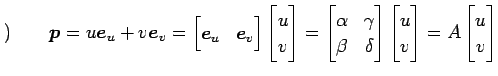 |
と表される. ベクトル
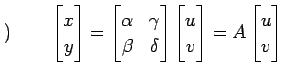 |
が成り立つ. 基底
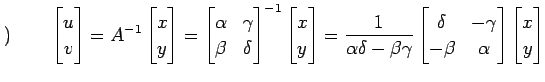 |
が成り立つ. (○)を座標
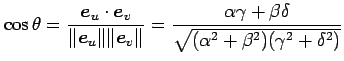 |
は一般には 0 とはならないので, 座標
問 2.78 (直交座標と斜交座標)
基底 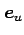 ,
, 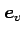 に関して次の問に答えよ.
に関して次の問に答えよ.
(1)
![]() と
と ![]() が直交する
が直交する
![]() ,
, ![]() ,
, ![]() ,
, ![]() の条件を求めよ.
の条件を求めよ.
(2)
![]() ,
, ![]() が単位ベクトルとなる
が単位ベクトルとなる
![]() ,
, ![]() ,
, ![]() ,
, ![]() の条件を求めよ.
の条件を求めよ.
(3)
![]() ,
, ![]() が直交しかつ単位ベクトルとなる
が直交しかつ単位ベクトルとなる
![]() ,
, ![]() ,
, ![]() ,
, ![]() の条件を求めよ.
の条件を求めよ.
例 2.79 (直交座標から斜交座標へのヤコビアン)
直交座標 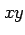 から斜交座標
から斜交座標 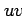 への座標変換(○)の
ヤコビアンを求める.
(○)より
への座標変換(○)の
ヤコビアンを求める.
(○)より
であるから,
となり, ヤコビアン
を得る.
であるから,
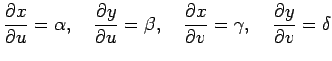 |
となり, ヤコビアン
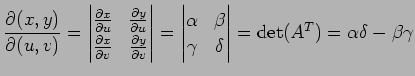 |
を得る.
例 2.80 (斜交座標における偏微分作用素)
直交座標 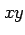 から斜交座標
から斜交座標 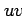 への座標変換(○)を考える.
関数
への座標変換(○)を考える.
関数 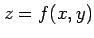 における
における 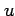 ,
, 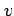 に関する偏導関数を求める.
導関数の微分則を用いると
に関する偏導関数を求める.
導関数の微分則を用いると
を得る.この関係式は
とも表される.また, ナブラ作用素
を導入すれば
と簡潔に表される. 次に(△)において関数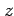 は任意でもよいので
関数を省略すると,
偏微分演算子の関係式
は任意でもよいので
関数を省略すると,
偏微分演算子の関係式
を得る. この関係式は偏微分作用素に関する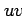 座標から
座標から 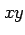 座標への変換を表す.
点に関する座標変換(○)の逆向きの変換であることに注意する.
座標への変換を表す.
点に関する座標変換(○)の逆向きの変換であることに注意する.
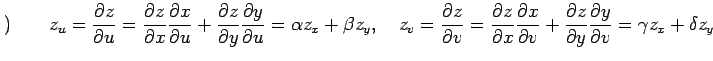 |
を得る.この関係式は
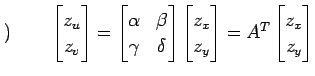 |
とも表される.また, ナブラ作用素
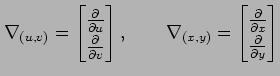 |
を導入すれば
と簡潔に表される. 次に(△)において関数
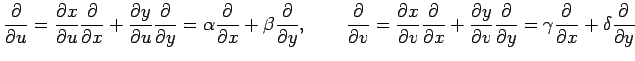 |
を得る. この関係式は偏微分作用素に関する
例 2.81 (斜交座標における偏微分作用素)
斜交座標 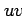 から直交座標
から直交座標 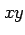 への座標変換(●)を考える.
関数
への座標変換(●)を考える.
関数 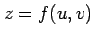 における
における  ,
, 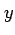 に関する偏導関数を求める.
(●)より座標変換は
に関する偏導関数を求める.
(●)より座標変換は
であるか,導関数の微分則を用いると
を得る.この関係式は
とも表される. この結果は(♭)の両辺に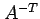 を左から
掛けることでも得られる.
また,ナブラ作用素を導入すると
を左から
掛けることでも得られる.
また,ナブラ作用素を導入すると
と簡潔に表される. 次に(▲)において関数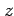 は任意で成り立つので
省略すると,
偏微分作用素の関係式
は任意で成り立つので
省略すると,
偏微分作用素の関係式
を得る. この関係式は偏微分作用素に関する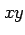 座標から
座標から 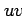 座標への変換を表す.
点に関する座標変換(●)の逆向きの変換であることに注意する.
座標への変換を表す.
点に関する座標変換(●)の逆向きの変換であることに注意する.
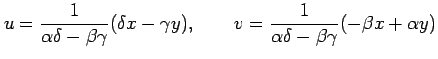 |
であるか,導関数の微分則を用いると
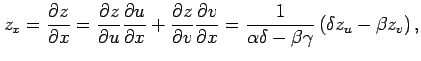 |
||
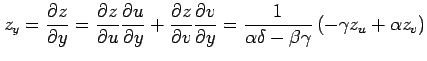 |
を得る.この関係式は
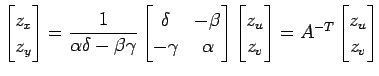 |
とも表される. この結果は(♭)の両辺に
と簡潔に表される. 次に(▲)において関数
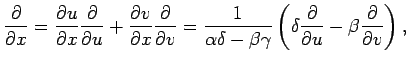 |
||
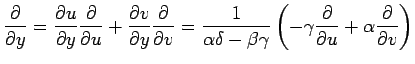 |
を得る. この関係式は偏微分作用素に関する
例 2.82 (斜交座標への座標変換)
関数 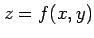 に対して関数
に対して関数
を考える. この関数を斜交座標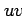 で表す.
(▲)を代入すると
で表す.
(▲)を代入すると
を得る.
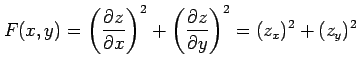 |
を考える. この関数を斜交座標
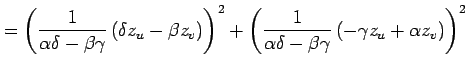 |
||
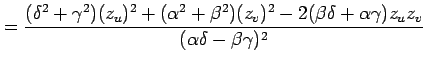 |
||
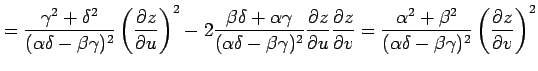 |
を得る.
問 2.83 (斜交座標への座標変換)
この関数 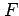 が斜交座標
が斜交座標 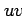 で
で
と表されるための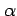 ,
, 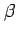 ,
, 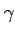 ,
, 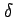 の必要十分条件は,
基底
の必要十分条件は,
基底 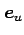 ,
, 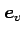 が
正規直交基底であることを示せ.
またこのとき,行列
が
正規直交基底であることを示せ.
またこのとき,行列 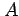 は直交行列となる(
は直交行列となる(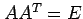 をみたす)
ことを示せ.
をみたす)
ことを示せ.
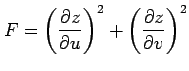 |
と表されるための
例 2.84 (斜交座標におけるラプラシアン)
関数 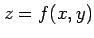 に対して関数
に対して関数
を考える. この関数を斜交座標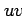 で表す.
(◎)より
で表す.
(◎)より
となるらか,
を得る.
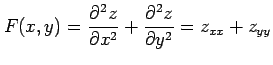 |
を考える. この関数を斜交座標
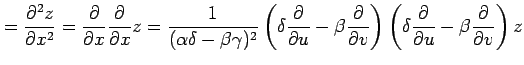 |
||
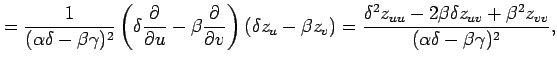 |
||
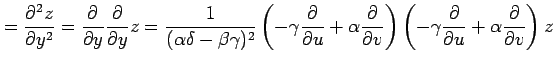 |
||
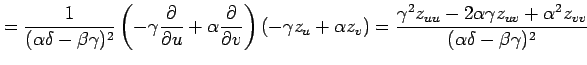 |
となるらか,
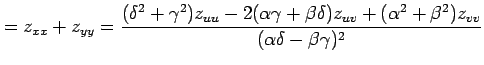 |
||
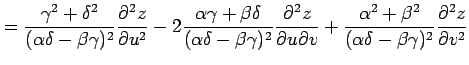 |
を得る.
例 2.85 (斜交座標におけるラプラシアン)
直交座標 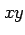 から斜交座標
から斜交座標 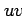 への座標変換(○)を考える.
このとき
ラプラシアン(Laplacian)または
ラプラス作用素(Laplace operator)
と呼ばれる
偏微分作用素
への座標変換(○)を考える.
このとき
ラプラシアン(Laplacian)または
ラプラス作用素(Laplace operator)
と呼ばれる
偏微分作用素
の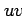 座標への変換を行う.
前例題において関数
座標への変換を行う.
前例題において関数 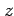 は任意であるから,
は任意であるから,
を得る.
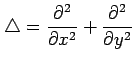 |
の
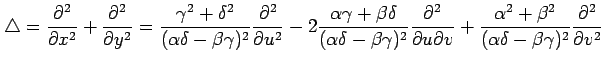 |
を得る.
問 2.86 (斜交座標におけるラプラシアン)
斜交座標 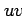 におけるラプラシアンが
におけるラプラシアンが
となるための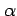 ,
, 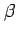 ,
, 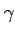 ,
, 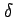 の必要十分条件は,
基底
の必要十分条件は,
基底 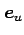 ,
, 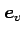 が
正規直交基底であることを示せ.
またこのとき,行列
が
正規直交基底であることを示せ.
またこのとき,行列 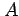 は直交行列となる(
は直交行列となる(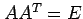 をみたす)
ことを示せ.
をみたす)
ことを示せ.
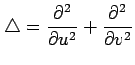 |
となるための
問 2.87 (斜交座標)
座標 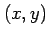 から斜交座標
から斜交座標 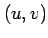 への座標変換
への座標変換
に対してそれぞれ,次の問に答えよ.
に対してそれぞれ,次の問に答えよ.
(i)
![]() ,
,
![]() をみたす
をみたす ![]() の軌跡をそれぞれ書け.
の軌跡をそれぞれ書け.
(ii)
![]() 軸(
軸(![]() の直線)と
の直線)と ![]() 軸(
軸(![]() の直線)の
方向ベクトルを求めよ.
の直線)の
方向ベクトルを求めよ.
(iii)
![]() 軸と
軸と ![]() 軸のなす角度を求めよ.
軸のなす角度を求めよ.
(iv)
座標
![]() に対して,
座標
に対して,
座標 ![]() を求めよ.
を求めよ.
(v)
座標
![]() に対して,
座標
に対して,
座標 ![]() を求めよ.
を求めよ.
(vi)
直線 ![]() を座標
を座標 ![]() で表せ.
で表せ.
(vii)
曲線 ![]() を座標
を座標 ![]() で表せ.
で表せ.
(viii)
ヤコビアン
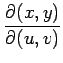 を求めよ.
を求めよ.
(ix)
偏微分作用素に関する座標 ![]() から座標
から座標 ![]() への
座標変換を求めよ.
への
座標変換を求めよ.
(x)
偏微分作用素に関する座標 ![]() から座標
から座標 ![]() への
座標変換を求めよ.
への
座標変換を求めよ.
(xi)
関数 ![]() に対する関数
に対する関数
![]() を座標
を座標 ![]() で表わせ.
で表わせ.
(xii)
関数 ![]() に対する関数
に対する関数
![]() を座標
を座標 ![]() で表わせ.
で表わせ.
(xiii)
ラプラス作用素
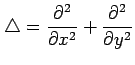 を座標
を座標 ![]() で表わせ.
で表わせ.
Kondo Koichi

平成18年1月18日