2.15 2 変数関数 と 1 変数関数の合成関数の微分
定理 2.63 (合成関数の微分)
2 変数関数 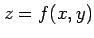 と 1 変数関数
と 1 変数関数 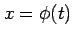 ,
, 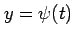 との
合成関数
との
合成関数
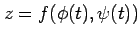 の導関数は
の導関数は
となる.また,代入も含めて正確に書くと
となる.
が成り立つ.または,
と表される. ただし,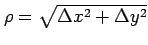 とおく.
このとき,
とおく.
このとき,
が成り立つ.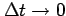 の極限をとると,
の極限をとると,
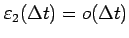 ,
,
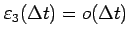 ,
,
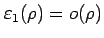 より,
より,
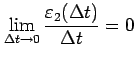 ,
,
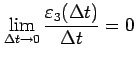 であり,
であり,
となるので,
を得る.
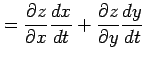 |
となる.また,代入も含めて正確に書くと
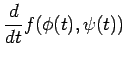 |
となる.
(証明)
関数 ![]() は全微分可能であり,
関数
は全微分可能であり,
関数 ![]() ,
, ![]() は微分可能とする.
このとき
は微分可能とする.
このとき
が成り立つ.または,
と表される. ただし,
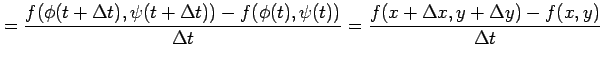 |
||
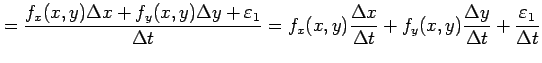 |
||
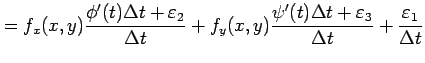 |
||
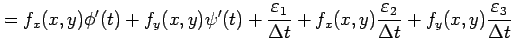 |
が成り立つ.
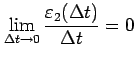 ,
,
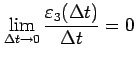 であり,
であり,
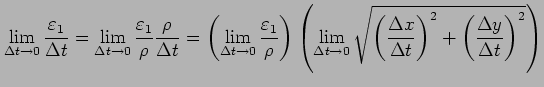 |
||
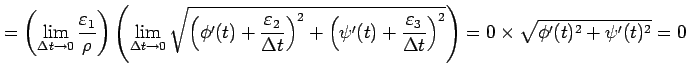 |
となるので,
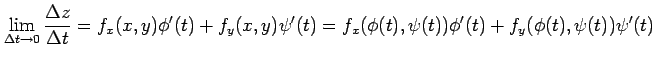 |
を得る.
例 2.64 (合成関数の微分)
関数 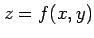 ,
, 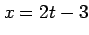 ,
, 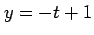 の合成関数
の合成関数
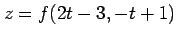 の導関数は,
の導関数は,
より
となる.
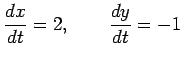 |
より
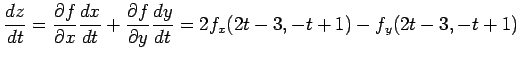 |
となる.
例 2.65 (合成関数の微分)
関数
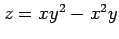 ,
, 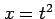 ,
, 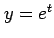 の
合成関数の導関数は,
の
合成関数の導関数は,
より
となる.
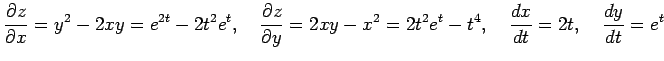 |
より
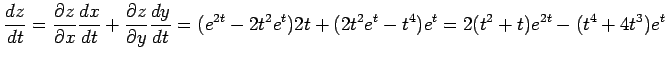 |
となる.
例 2.66 (合成関数の微分)
関数 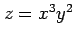 ,
, 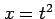 ,
, 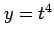 の合成関数の微分は,
の合成関数の微分は,
より
となる.
より
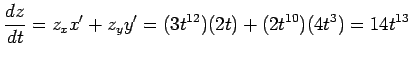 |
となる.
例 2.67 (合成関数の微分)
関数 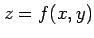 ,
, 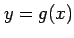 の
合成関数
の
合成関数
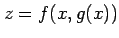 の
の  微分を考える.
まず,
微分を考える.
まず,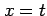 ,
, 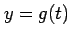 と置き換えて,
と置き換えて,
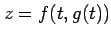 を
を 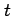 で微分する.
で微分する.
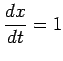 ,
,
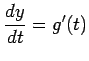 より
より
となる.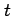 を
を  に置き換えると
に置き換えると
を得る.
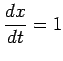 ,
,
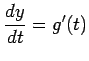 より
より
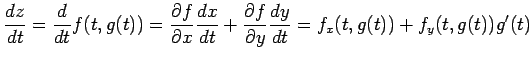 |
となる.
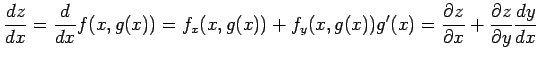 |
を得る.
問 2.68 (合成関数の微分)
次の合成関数の導関数を求めよ.
(1)
![]() ,
, ![]() ,
, ![]() (2)
(2)
![]() ,
, ![]() ,
, ![]()
Kondo Koichi

平成18年1月18日