2.22 2 次元空間の極座標
定義 2.88 (極座標)
2 次元空間において,
直交座標 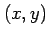 から
極座標(polar coordinates)
から
極座標(polar coordinates)
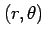 への
座標変換は
への
座標変換は
で与えられる.
で与えられる.
注意 2.89 (極座標)
極座標
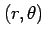 から
直交座標
から
直交座標 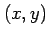 への座標変換は
への座標変換は
と表される.
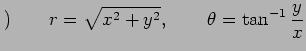 |
と表される.
![\includegraphics[width=0.5\textwidth]{polar2.eps}](img761.png)
例 2.90 (極座標のヤコビアン)
座標変換(☆)より
となるらか,ヤコビアンは
と得られる.
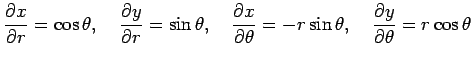 |
となるらか,ヤコビアンは
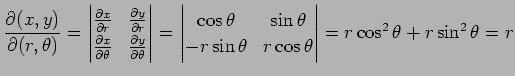 |
と得られる.
例 2.91 (極座標における偏微分作用素の変換)
座標 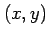 から極座標
から極座標
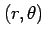 への変換(☆)を考える.
関数
への変換(☆)を考える.
関数 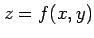 を
を 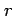 ,
, 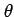 に関して偏微分すると,
合成関数の微分則より
に関して偏微分すると,
合成関数の微分則より
が成り立つ.これは
とも表される. 行列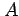 の行列式がヤコビアンである.
このとき,
の行列式がヤコビアンである.
このとき,
と書くと関数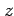 は任意であり省略すると
は任意であり省略すると
となる. (★)を用いて右辺の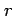 ,
, 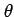 を
を  ,
, 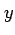 で表すと
で表すと
となる. これは偏微分作用素における 極座標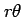 から座標
から座標 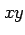 への座標変換である.
点に関する座標変換(☆)とは
変換の向きが異なることに注意する.
への座標変換である.
点に関する座標変換(☆)とは
変換の向きが異なることに注意する.
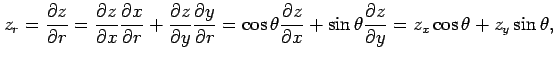 |
||
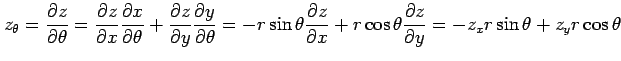 |
が成り立つ.これは
 |
とも表される. 行列
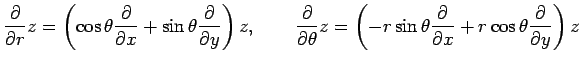 |
と書くと関数
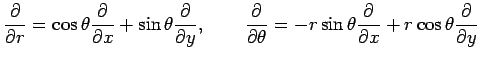 |
となる. (★)を用いて右辺の
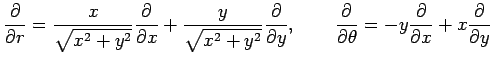 |
となる. これは偏微分作用素における 極座標
例 2.92 (極座標における偏微分作用素の変換)
極座標
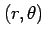 から座標
から座標 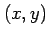 への変換(★)を考える.
関数
への変換(★)を考える.
関数
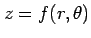 を
を  ,
, 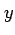 に関して偏微分すると,
(★)と合成関数の微分則より
に関して偏微分すると,
(★)と合成関数の微分則より
が成り立つ. さらに(☆)を用いて右辺を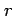 ,
, 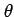 で表すと
で表すと
となる. これは
とも表される. この式は(♭)の両辺に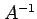 を左から掛けることでも
得られる.すなわち,
を左から掛けることでも
得られる.すなわち,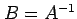 となる.
ここで,
となる.
ここで,
と書くと,関数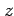 は任意であり省略すると
は任意であり省略すると
を得る. これは偏微分作用素における 座標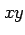 から極座標
から極座標 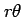 への座標変換である.
点に関する座標変換(★)とは
変換の向きが異なることに注意する.
への座標変換である.
点に関する座標変換(★)とは
変換の向きが異なることに注意する.
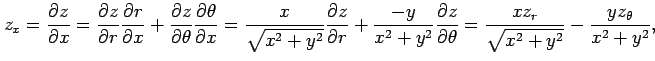 |
||
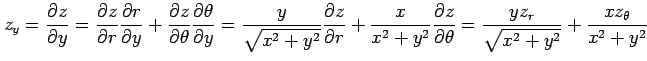 |
が成り立つ. さらに(☆)を用いて右辺を
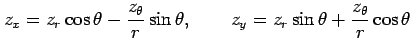 |
となる. これは
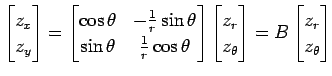 |
とも表される. この式は(♭)の両辺に
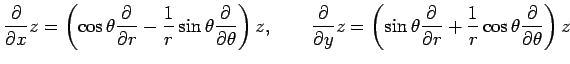 |
と書くと,関数
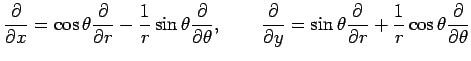 |
を得る. これは偏微分作用素における 座標
例 2.93 (極座標への座標変換)
関数 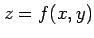 に対して関数
に対して関数
を考える. この関数を極座標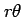 で表す.
(▲)を代入すると
で表す.
(▲)を代入すると
を得る.
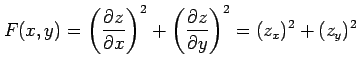 |
を考える. この関数を極座標
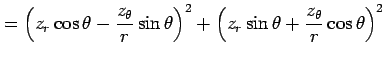 |
||
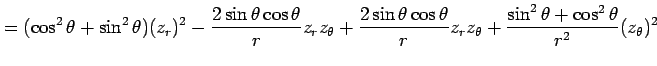 |
||
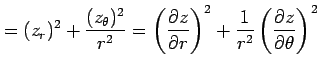 |
を得る.
例 2.94 (極座標におけるラプラシアン)
関数 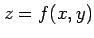 に対して関数
に対して関数
を考える. この関数を極座標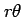 で表す.
(○)より,
で表す.
(○)より,
となる. よって
を得る.
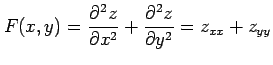 |
を考える. この関数を極座標
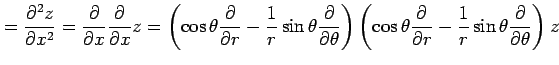 |
||
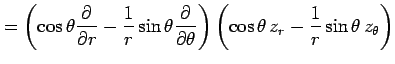 |
||
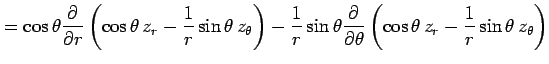 |
||
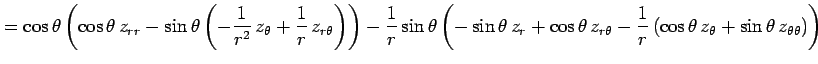 |
||
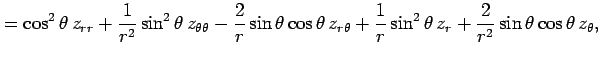 |
||
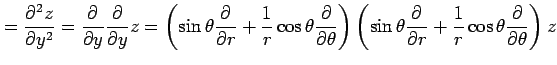 |
||
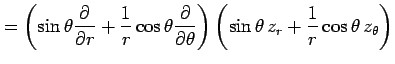 |
||
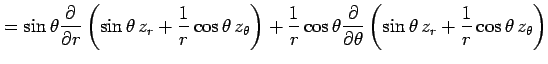 |
||
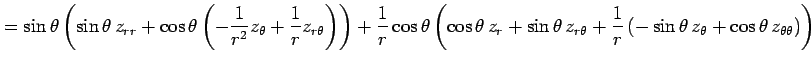 |
||
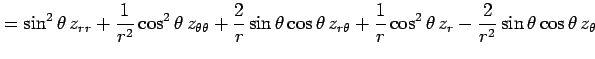 |
となる. よって
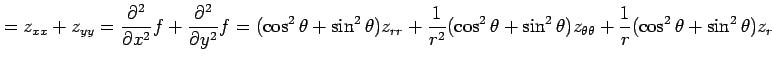 |
||
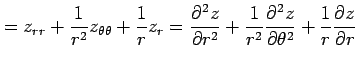 |
を得る.
例 2.95 (極座標におけるラプラシアン)
ラプラス演算子
を座標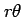 で表す.
前例題より
で表す.
前例題より
が成り立つ.関数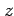 は任意であるから,
は任意であるから,
を得る.
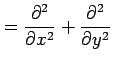 |
を座標
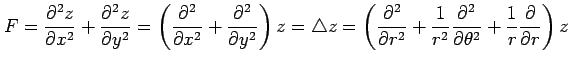 |
が成り立つ.関数
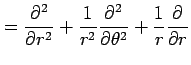 |
を得る.
Kondo Koichi

平成18年1月18日