2.3 連続性
定義 2.15 (連続)
関数 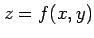 は次の条件(i), (ii), (iii)をみたすとき
点
は次の条件(i), (ii), (iii)をみたすとき
点 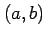 で連続(continuous)であるという.
で連続(continuous)であるという.
- (i).
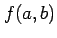 が定義されている.
が定義されている.
- (ii).
- 極限
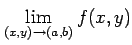 が存在する.
が存在する.
- (iii).
-
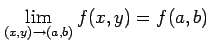 が成り立つ.
が成り立つ.
例 2.16 (連続の具体例)
関数
は原点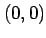 で連続であるか調べる.
(i)
で連続であるか調べる.
(i) 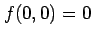 と定義されている.
(ii) 前述の例題により,極限
と定義されている.
(ii) 前述の例題により,極限
が存在する. (iii) (i), (ii) より
が成り立つ. 以上,(i), (ii), (iii)より 関数 は原点
は原点 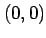 で連続である.
で連続である.
![$\displaystyle f(x,y)= \left\{ \begin{array}{ll} \displaystyle{\frac{x^3+y^3}{x^2+y^2}} & ((x,y)\neq(0,0)) \\ [3ex] 0 & ((x,y)=(0,0)) \end{array} \right.$](img249.png) |
は原点
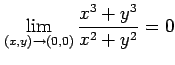 |
が存在する. (iii) (i), (ii) より
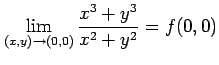 |
が成り立つ. 以上,(i), (ii), (iii)より 関数
例 2.17 (不連続の具体例)
関数
は原点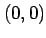 で連続であるか調べる.
まず,極限が存在するか調べる.
直線
で連続であるか調べる.
まず,極限が存在するか調べる.
直線 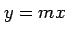 に沿って近づけると,
に沿って近づけると,
となる. 直線の傾き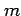 が異なれば,
収束する値
が異なれば,
収束する値
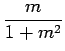 も異なる.
よって
も異なる.
よって
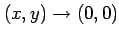 における極限は存在しない.
極限が存在しないので,原点
における極限は存在しない.
極限が存在しないので,原点 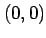 で
で  は連続ではない.
は連続ではない.
![$\displaystyle f(x,y)= \left\{ \begin{array}{ll} \displaystyle{\frac{xy}{x^2+y^2}} & ((x,y)\neq(0,0)) \\ [3ex] 0 & ((x,y)=(0,0)) \end{array} \right.$](img252.png) |
は原点
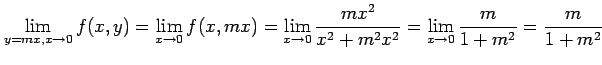 |
となる. 直線の傾き
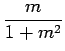 も異なる.
よって
も異なる.
よって
例 2.18 (不連続の具体例)
関数
は原点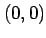 で連続であるか考える.
まず,
前述の例題により,極限
で連続であるか考える.
まず,
前述の例題により,極限
が存在する. しかし,原点で値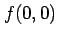 が定義されていない.
よって関数
が定義されていない.
よって関数  は原点
は原点  で不連続である.
で不連続である.
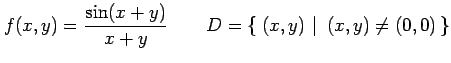 |
は原点
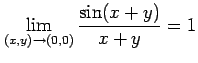 |
が存在する. しかし,原点で値
注意 2.19 (除きうる不連続点)
関数
は原点で不連続である. しかし,不連続点 において
において
と定義する. すると,関数 は
は
をみたし,原点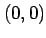 で連続となる.
このように定義を加えることで連続となる
不連続点のことを
除きうる不連続点(removable discontinuity)という.
で連続となる.
このように定義を加えることで連続となる
不連続点のことを
除きうる不連続点(removable discontinuity)という.
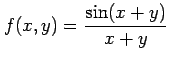 |
は原点で不連続である. しかし,不連続点
と定義する. すると,関数
をみたし,原点
問 2.20 (連続)
次の関数  は原点
は原点 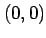 で連続であるか述べよ.
除きうる不連続点の場合は,
で連続であるか述べよ.
除きうる不連続点の場合は,
 が連続となるよう
が連続となるよう 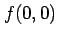 を定義せよ.
を定義せよ.
(1) ![]() (2)
(2)
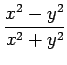 (3)
(3)
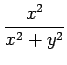 (4)
(4)
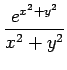 (5)
(5)
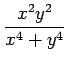
Kondo Koichi

平成18年1月18日