2.35 極値
定義 2.149 (極値)
関数  が,
点
が,
点 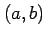 とその任意の近傍の点
とその任意の近傍の点 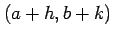 に対して
に対して
をみたすとき, は点
は点 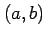 で
極大値
で
極大値 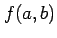 をとるという.
また,
をとるという.
また,
をみたすとき, は点
は点 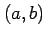 で
極小値
で
極小値 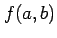 をとるという.
極大値,極小値を総称して極値という.
をとるという.
極大値,極小値を総称して極値という.
をみたすとき,
をみたすとき,
定理 2.150 (極値の必用条件)
関数  が点
が点 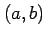 で極値をとるとき,
で極値をとるとき,
が成り立つ. (注意)逆は成り立たない.
が成り立つ. (注意)逆は成り立たない.
(証明)
平面 ![]() と曲面
と曲面 ![]() との共有点からなる曲線
との共有点からなる曲線 ![]() は
は
![]() についての 1 変数関数であり,
についての 1 変数関数であり,
![]() が極値をとるとき
が極値をとるとき ![]() も極値をとる.
よって,
も極値をとる.
よって,
![]() となる.
同様にして,平面
となる.
同様にして,平面 ![]() を考えると
を考えると
![]() を得る.
を得る.
注意 2.151 (極値と接平面)
関数  は点
は点 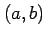 で極値をとるとする.
このとき
で極値をとるとする.
このとき
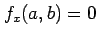 ,
,
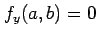 であるから,
であるから,
 を点
を点 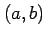 のまわりでテイラー展開すると
のまわりでテイラー展開すると
となり,1 次の項は存在しない. また, 曲面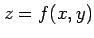 の点
の点 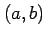 における接平面の方程式は
における接平面の方程式は
となり,法線ベクトルは
である.接平面は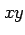 平面に平行である.
平面に平行である.
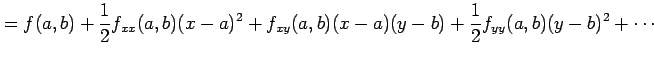 |
となり,1 次の項は存在しない. また, 曲面
となり,法線ベクトルは
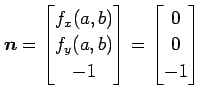 |
である.接平面は
例 2.152 (極値の計算例)
関数
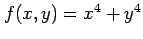 の極値を考える.
連立方程式
の極値を考える.
連立方程式
を解くと候補の点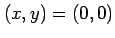 を得る.
このとき点
を得る.
このとき点 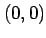 とその任意の近傍の点
とその任意の近傍の点 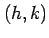 に対して,
に対して,
が成り立つ. よって関数 は極小値
は極小値 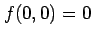 をとる.
をとる.
を解くと候補の点
が成り立つ. よって関数
例 2.153 (鞍点)
関数
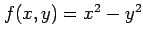 の極値を考える.
連立方程式
の極値を考える.
連立方程式
を解くと候補の点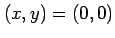 を得る.
しかし,
を得る.
しかし,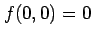 は極値とはならない.
なぜなら,点
は極値とはならない.
なぜなら,点 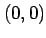 と
と  軸方向にずれた近傍の点
軸方向にずれた近傍の点 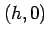 に対しては,
に対しては,
となり,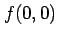 は極小となる.
一方,
点
は極小となる.
一方,
点 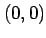 と
と 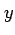 軸方向にずれた近傍の点
軸方向にずれた近傍の点 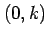 に対しては,
に対しては,
となり,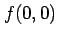 は極大となる.
このようにある方向では極小であり,
また別の方向では極大となる点のことを
鞍点(saddle point)という.
は極大となる.
このようにある方向では極小であり,
また別の方向では極大となる点のことを
鞍点(saddle point)という.
![\includegraphics[width=0.7\textwidth]{saddle.eps}](img1143.png)
を解くと候補の点
となり,
となり,
![\includegraphics[width=0.7\textwidth]{saddle.eps}](img1143.png)
定理 2.154 (極値)
関数  において点
において点 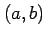 が
が
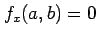 ,
,
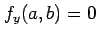 をみたすとき,
をみたすとき,
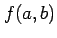 が極値となるための判定条件は次の通りである.
ただし,
が極値となるための判定条件は次の通りである.
ただし,
とおく.
とおく.
- (i).
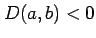 ,
,
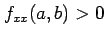 のとき,
のとき,
 は点
は点 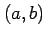 で極小値をとる.
で極小値をとる.
- (ii).
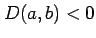 ,
,
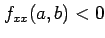 のとき,
のとき,
 は点
は点 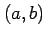 で極大値をとる.
で極大値をとる.
- (iii).
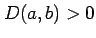 のとき,
のとき,
 は点
は点 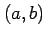 で極値をとらない.
で極値をとらない.
- (iv).
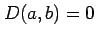 のとき,個別に判定する.
のとき,個別に判定する.
(証明) typing...
例 2.155 (極値の計算例)
関数
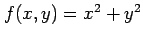 の極値を求める.
連立方程式
の極値を求める.
連立方程式
を解くと極値の候補として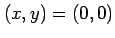 を得る.このとき,
を得る.このとき,
となる. よって,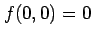 は極小値である.
は極小値である.
を解くと極値の候補として
となる. よって,
例 2.156 (極値の計算例)
関数
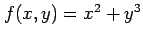 の極値を求める.
連立方程式
の極値を求める.
連立方程式
を解くと極値の候補として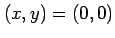 を得る.このとき,
を得る.このとき,
となる.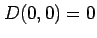 であるから判別式
であるから判別式 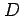 を用いて極値となるかは判定できない.
そこで,点
を用いて極値となるかは判定できない.
そこで,点 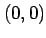 と
その近傍の点
と
その近傍の点 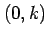 ,
, 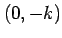 を考える.
ただし,
を考える.
ただし, 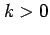 とする.
このとき,
とする.
このとき,
が成り立つ. 点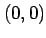 から
から 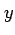 軸正の方向には増加傾向であり,
軸正の方向には増加傾向であり,
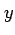 軸負の方向には減少傾向となるので,
軸負の方向には減少傾向となるので,
 は極値ではない.
は極値ではない.
![\includegraphics[width=0.7\textwidth]{kyokuchi.eps}](img1163.png)
を解くと極値の候補として
となる.
が成り立つ. 点
![\includegraphics[width=0.7\textwidth]{kyokuchi.eps}](img1163.png)
例 2.157 (極値の計算例)
関数
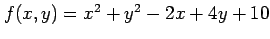 の極値を求める.
連立方程式
の極値を求める.
連立方程式
を解くと極値の候補として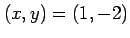 を得る.このとき,
を得る.このとき,
となる. よって,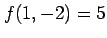 は極小値である.
は極小値である.
を解くと極値の候補として
となる. よって,
例 2.158 (極値の計算例)
関数
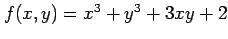 の極値を求める.
連立方程式
の極値を求める.
連立方程式
を解く. 第 1 式を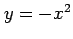 と変形して第 2 式に代入すると
と変形して第 2 式に代入すると
となる.これを解くと,極値の候補として
を得る.このとき,
を用いて極値であるか判定する. まず,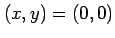 の場合.
の場合.
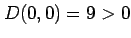 より
より 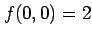 は極値ではない.
次に,
は極値ではない.
次に,
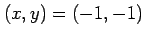 の場合.
の場合.
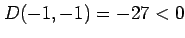 ,
,
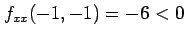 より,
より,
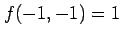 は極大値である.
は極大値である.
![\includegraphics[width=0.7\textwidth]{kyokuchi2.eps}](img1180.png)
を解く. 第 1 式を
となる.これを解くと,極値の候補として
を得る.このとき,
を用いて極値であるか判定する. まず,
![\includegraphics[width=0.7\textwidth]{kyokuchi2.eps}](img1180.png)
問 2.159 (極値)
次の関数の極値を求めよ.
(1)
![]() (2)
(2)
![]()
Kondo Koichi

平成18年1月18日