2.20 座標変換
定義 2.75 (座標変換)
座標
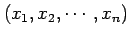 が
変数
が
変数
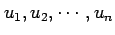 を独立変数とする関数
を独立変数とする関数
により定まるとする. このとき,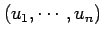 をあらたに座標と呼び,
(*)を座標
をあらたに座標と呼び,
(*)を座標
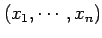 から
座標
から
座標
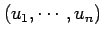 への
座標変換(coordinate transform)と呼ぶ.
への
座標変換(coordinate transform)と呼ぶ.
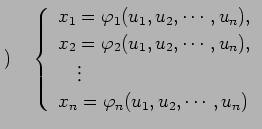 |
により定まるとする. このとき,
定義 2.76 (ヤコビアン)
座標変換
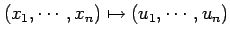 に対して,
行列式
に対して,
行列式
をこの座標変換のヤコビアン(Jacobian) またはヤコビの行列式(Jacobi determinant)という.
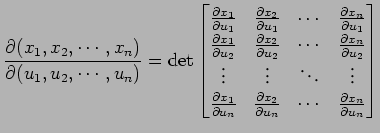 |
をこの座標変換のヤコビアン(Jacobian) またはヤコビの行列式(Jacobi determinant)という.
注意 2.77 (座標変換)
ヤコビアンが非零となるときのみ,
座標 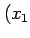 ,
, 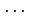 ,
, 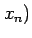 と
座標
と
座標 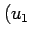 ,
, 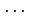 ,
, 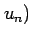 とが 1 対 1 に対応する.
とが 1 対 1 に対応する.
Kondo Koichi

平成18年1月18日