2.24 調和関数
定義 2.102 (ラプラス演算子)
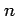 次元座標
次元座標
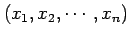 の空間の
ラプラス演算子(Laplace operator)または
ラプラシアン(Laplacian)は
の空間の
ラプラス演算子(Laplace operator)または
ラプラシアン(Laplacian)は
により定義される.
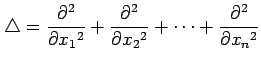 |
により定義される.
定義 2.103 (調和関数)
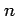 変数関数
変数関数
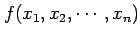 が
が
をみたすとき,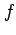 を調和関数(harmonic function)という.
を調和関数(harmonic function)という.
をみたすとき,
例 2.104 (調和関数)
関数
は調和関数である. typing...
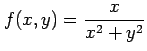 |
は調和関数である. typing...
極座標で表すと, typing...
例 2.105 (調和関数)
関数
は調和関数である. typing...
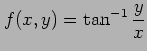 |
は調和関数である. typing...
極座標で表すと, typing...
例 2.106 (調和関数)
関数
は調和関数である. typing...
は調和関数である. typing...
極座標で表すと, typing...
Kondo Koichi

平成18年1月18日