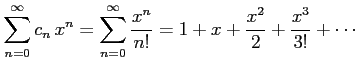4.23 べき級数
定義 4.95 (べき級数)
定数
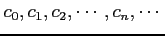 と
変数
と
変数 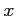 を考える.
このとき級数
を考える.
このとき級数
をべき級数(power series)または 整級数(polynomial series)と呼ぶ. 同様に級数
を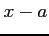 のべき級数と呼ぶ.
のべき級数と呼ぶ.
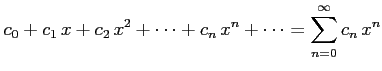 |
をべき級数(power series)または 整級数(polynomial series)と呼ぶ. 同様に級数
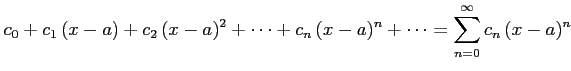 |
を
定理 4.96 (べき級数)
級数
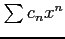 が
が 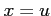 で収束するとき,
絶対級数
で収束するとき,
絶対級数
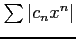 は
は 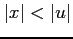 で収束する.
よって級数
で収束する.
よって級数
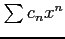 も
も 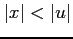 で収束する.
で収束する.
(証明)
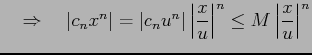 |
||
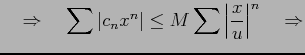
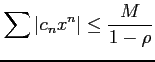 |
||
定義 4.97 (収束半径)
べき級数
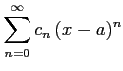 は
は
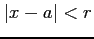 において絶対収束し,
において絶対収束し,
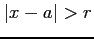 において発散する.
定数
において発散する.
定数 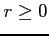 を収束半径(radius of convergence)と呼ぶ.
を収束半径(radius of convergence)と呼ぶ.
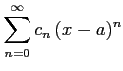 は
は
例 4.98 (収束半径の具体例)
べき級数
を考える.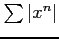 は
は 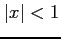 のとき収束する
(公比が
のとき収束する
(公比が 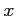 の等比級数であるから).
よって
の等比級数であるから).
よって 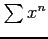 は
は 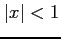 のとき絶対収束する.
よって収束半径は
のとき絶対収束する.
よって収束半径は 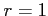 である.
である.
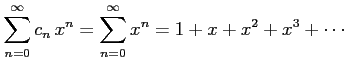 |
を考える.
定理 4.100 (収束半径の計算法)
べき級数
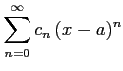 を考える.
極限
を考える.
極限
または
が存在するとき, べき級数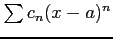 の収束半径は
の収束半径は 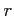 である.
である.
であるので,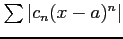 が収束するとき
が収束するとき
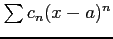 も収束する.
も収束する.
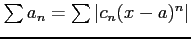 とおくと,
とおくと,
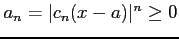 であるから
であるから
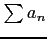 は正項級数となる.
ゆえにダランベールの
収束判定法(定理
は正項級数となる.
ゆえにダランベールの
収束判定法(定理 ![[*]](crossref.png) )より,
級数
)より,
級数
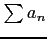 は
は
のとき収束する. よって
となる. これより
を得る. 以上より収束半径は
と求まる. 同様にしてコーシーの 収束判定法(定理![[*]](crossref.png) )より
)より
![$ \displaystyle{r=\lim_{n\to\infty}1/\sqrt[n]{\vert c_{n}\vert}}$](img1928.png) が求まる.
が求まる.
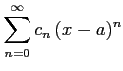 を考える.
極限
を考える.
極限
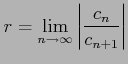 |
または
![$\displaystyle r=\lim_{n\to\infty} \frac{1}{\sqrt[n]{\vert c_{n}\vert}}$](img1913.png) |
が存在するとき, べき級数
(証明)
級数
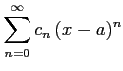 と
その絶対級数
と
その絶対級数
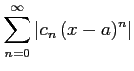 を
考える.
このとき
を
考える.
このとき
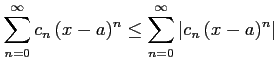 |
であるので,
![[*]](crossref.png) )より,
級数
)より,
級数
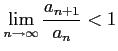 |
のとき収束する. よって
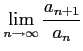 |
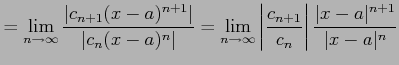 |
|
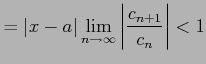 |
となる. これより
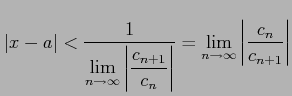 |
を得る. 以上より収束半径は
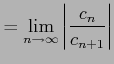 |
と求まる. 同様にしてコーシーの 収束判定法(定理
![[*]](crossref.png) )より
)より
例 4.101 (収束半径の計算例)
べき級数
の収束半径を求める.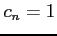 であるから,収束半径は
であるから,収束半径は
と求まる. べき級数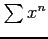 は
は
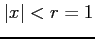 のとき収束し,
のとき収束し,
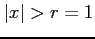 のとき発散する.
のとき発散する.
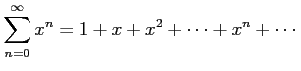 |
の収束半径を求める.
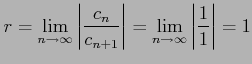 |
と求まる. べき級数
例 4.102 (収束半径の計算例)
べき級数
の収束半径を求める.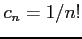 であるから,収束半径は
であるから,収束半径は
と求まる.収束半径は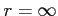 である.
べき級数
である.
べき級数
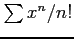 は任意の実数
は任意の実数 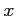 に対して収束する.
に対して収束する.
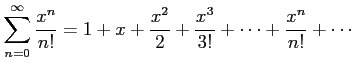 |
の収束半径を求める.
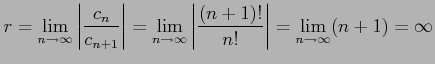 |
と求まる.収束半径は
例 4.103 (収束半径の計算例)
べき級数
の収束半径を求める.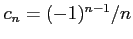 であるから,
収束半径は
であるから,
収束半径は
と求まる. べき級数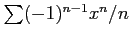 は
は
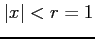 のとき収束し,
のとき収束し,
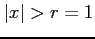 のとき発散する.
のとき発散する.
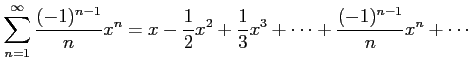 |
の収束半径を求める.
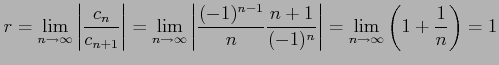 |
と求まる. べき級数
例 4.104 (収束半径の計算例)
べき級数
の収束半径を求める.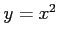 とおくと,べき級数は
とおくと,べき級数は
と書ける.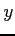 の級数の収束半径は,
の級数の収束半径は,
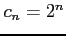 とおくと
とおくと
と求まる.級数は
のとき収束する. よって,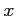 については
については
のとき収束するので,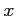 についての収束半径は
についての収束半径は
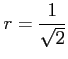 である.
である.
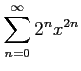 |
の収束半径を求める.
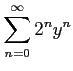 |
と書ける.
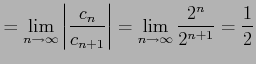 |
と求まる.級数は
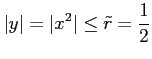 |
のとき収束する. よって,
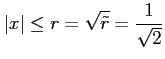 |
のとき収束するので,
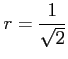 である.
である.
平成21年6月1日