4.19 正項級数に関するダランベールの収束判定法
定理 4.74 (ダランベールの収束判定法)
正項級数
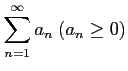 は,
極限
は,
極限
により,級数の収束性の判定ができる:
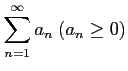 は,
極限
は,
極限
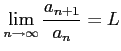 |
により,級数の収束性の判定ができる:
- (i)
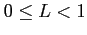 のとき,
のとき,
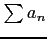 は収束する.
は収束する.
- (ii)
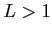 のとき,
のとき,
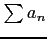 は発散する.
は発散する.
- (iii)
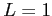 のとき,
のとき,
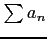 の収束性は判定できない.
の収束性は判定できない.
例 4.75 (ダランベールの判定法の具体例)
級数
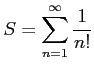 を考える.
を考える.
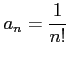 とおくと,
とおくと,
が成り立つ. ダランベールの収束判定法を用いる.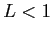 であるから
であるから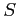 は収束する.
は収束する.
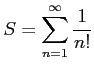 を考える.
を考える.
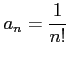 とおくと,
とおくと,
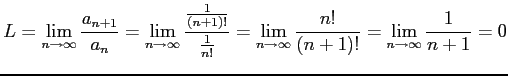 |
が成り立つ. ダランベールの収束判定法を用いる.
例 4.76 (ダランベールの判定法の具体例)
級数
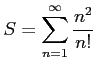 を考える.
を考える.
より,ダランベールの収束判定法を用いると,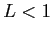 であるから
であるから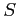 は収束する.
は収束する.
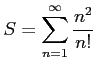 を考える.
を考える.
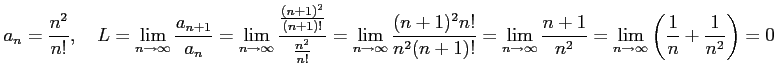 |
より,ダランベールの収束判定法を用いると,
例 4.77 (ダランベールの判定法の具体例)
級数
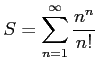 を考える.
を考える.
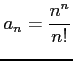 より
より
となり,ダランベールの収束判定法を用いると,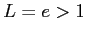 であるから
であるから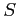 は発散する.
は発散する.
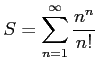 を考える.
を考える.
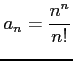 より
より
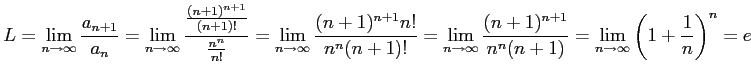 |
となり,ダランベールの収束判定法を用いると,
例 4.78 (ダランベールの判定法の具体例)
級数
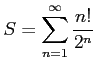 を考える.
を考える.
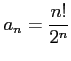 より
より
となり,ダランベールの収束判定法を用いると,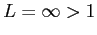 であるから
であるから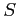 は発散する.
は発散する.
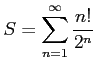 を考える.
を考える.
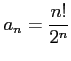 より
より
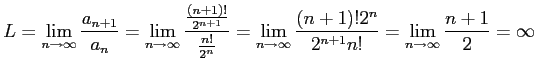 |
となり,ダランベールの収束判定法を用いると,
例 4.79 (ダランベールの判定法の具体例)
級数
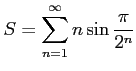 を考える.
を考える.
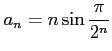 より
より
となり,ダランベールの収束判定法を用いると,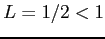 であるから
であるから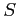 は収束する.
は収束する.
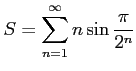 を考える.
を考える.
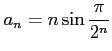 より
より
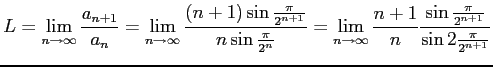 |
||
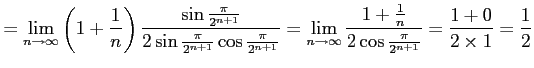 |
となり,ダランベールの収束判定法を用いると,
例 4.80 (ダランベールの判定法の具体例)
級数
を考える.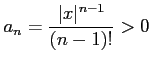 であるから,
であるから,
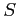 は正項級数である.
よって
は正項級数である.
よって
が成り立つので,ダランベールの判定法より級数は収束する.
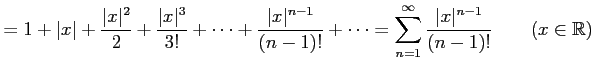 |
を考える.
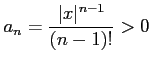 であるから,
であるから,
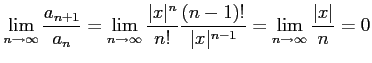 |
が成り立つので,ダランベールの判定法より級数は収束する.
例 4.81 (ダランベールの判定法で判定できない例)
調和級数
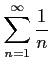 を考える.
隣り合う項の比の極限は
を考える.
隣り合う項の比の極限は
となるのでダランベールの判定法定法では判定できない. 前述のように別の方法で行う.
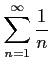 を考える.
隣り合う項の比の極限は
を考える.
隣り合う項の比の極限は
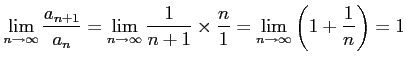 |
となるのでダランベールの判定法定法では判定できない. 前述のように別の方法で行う.
平成21年6月1日