4.20 正項級数に関するコーシーの収束判定法
定理 4.82 (コーシーの収束判定法)
正項級数
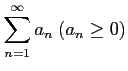 は,
極限
は,
極限
により,級数の収束性の判定ができる:
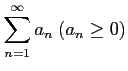 は,
極限
は,
極限
により,級数の収束性の判定ができる:
- (i)
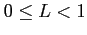 のとき,
のとき,
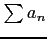 は収束する.
は収束する.
- (ii)
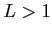 のとき,
のとき,
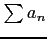 は発散する.
は発散する.
- (iii)
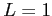 のとき,
のとき,
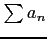 の収束性は判定できない.
の収束性は判定できない.
例 4.83 (コーシーの収束判定法)
級数
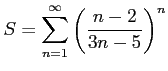 を考える.
を考える.
が成り立つので, コーシーの収束判定法より,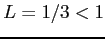 となるので
となるので 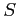 は収束する.
は収束する.
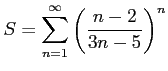 を考える.
を考える.
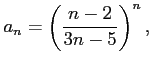 |
||
![$\displaystyle L= \lim_{n\to\infty}\sqrt[n]{a_n}= \lim_{n\to\infty}\sqrt[n]{\lef...
...{n-2}{3n-5}= \lim_{n\to\infty}\frac{1-2/n}{3-5/n}= \frac{1-0}{3-0}= \frac{1}{3}$](img1844.png) |
が成り立つので, コーシーの収束判定法より,
例 4.84 (コーシーの収束判定法)
級数
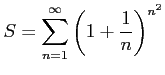 を考える.
を考える.
が成り立つので, コーシーの収束判定法より,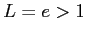 となるので
となるので 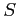 は発散する.
は発散する.
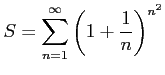 を考える.
を考える.
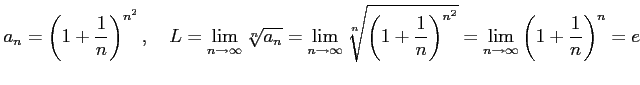 |
が成り立つので, コーシーの収束判定法より,
平成21年6月1日