1.38 ちょっとまとめ
まとめ 1.180 (直線,平面)
同じ記号が同じ形である.
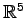 において,
において,
![]() において,
において,
点:
![]()
![]() (○)
(○)![]()
直線:
![]()
![]() (□)
(□) ![]()
![]() において,
において,
点:
![]()
![]() (○)
(○)
![]()
直線:
![]()
![]() (△)
(△)
![]()
![]() (◎)
(◎)
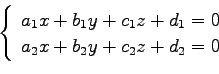
平面:
![]()
![]()
![]()
![]() (□)
(□)
![]()
![]() において,
において,
| 点: |
||||
| 直線: |
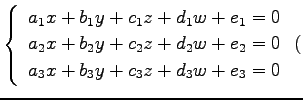 ◎ ◎ |
|||
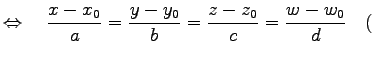 △ △ |
||||
| 平面: |
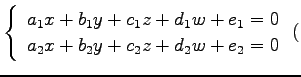 ◎ ◎ |
|||
| 超平面: |
||||
| 点: |
||||
| 直線: |
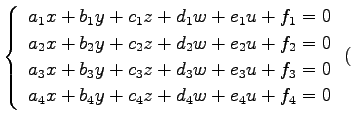 ◎ ◎ |
|||
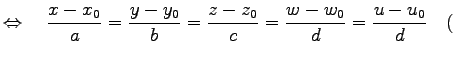 △ △ |
||||
| 平面: |
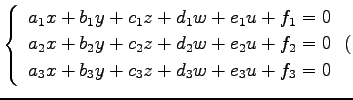 ◎ ◎ |
|||
| 超平面: |
||||
平成20年2月2日