1.37 平面と平面の交線
注意 1.177 (平面と平面の共通集合は直線)
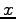 ,
, 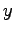 ,
, 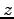 に関する非同次 1 次方程式の一般形は
に関する非同次 1 次方程式の一般形は
である.この方程式は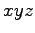 空間内の
法線ベクトルが
空間内の
法線ベクトルが
![$ \begin{bmatrix}{a}\\ [-.5ex]{b}\\ [-.5ex]{c}\end{bmatrix}$](img906.png) で点
で点
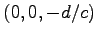 を通る平面を表す.
非同次 1 次方程式を 2 本の方程式で連立すると
を通る平面を表す.
非同次 1 次方程式を 2 本の方程式で連立すると
である.方程式のそれぞれは法線ベクトルが![$ \begin{bmatrix}{a_1}\\ [-.5ex]{b_1}\\ [-.5ex]{c_1}\end{bmatrix}$](img909.png) と
と
![$ \begin{bmatrix}{a_2}\\ [-.5ex]{b_2}\\ [-.5ex]{c_2}\end{bmatrix}$](img910.png) の
平面を表す.
よって,
この連立方程式の解集合は,
2 つの平面の共有点の集合である直線
の
平面を表す.
よって,
この連立方程式の解集合は,
2 つの平面の共有点の集合である直線
となる. ただし, 交線をもつのは 法線ベクトル![$ \begin{bmatrix}{a_1}\\ [-.5ex]{b_1}\\ [-.5ex]{c_1}\end{bmatrix}$](img909.png) と
と
![$ \begin{bmatrix}{a_1}\\ [-.5ex]{b_1}\\ [-.5ex]{c_1}\end{bmatrix}$](img909.png) とが同じ向きではないときに限られる.
とが同じ向きではないときに限られる.
である.この方程式は
である.方程式のそれぞれは法線ベクトルが
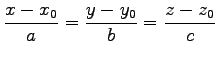 |
(244) |
となる. ただし, 交線をもつのは 法線ベクトル
例 1.178 (平面と平面の交線)
二つの平面
の交線を求める. 第一式を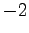 倍し第二式の加えると
倍し第二式の加えると
となる. 第二式を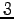 で割ると
で割ると
となる. 第二式を第一式に加えると
となる.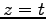 とおくと
とおくと
を得る. 交線は点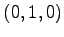 を通る
方向ベクトル
を通る
方向ベクトル
![$ \begin{bmatrix}{-1}\\ [-.5ex]{-2}\\ [-.5ex]{1}\end{bmatrix}$](img917.png) の直線である.
の直線である.
| (245) |
の交線を求める. 第一式を
| (246) |
となる. 第二式を
| (247) |
となる. 第二式を第一式に加えると
| (248) |
となる.
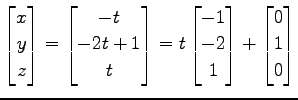 |
(249) |
を得る. 交線は点
![$ \begin{bmatrix}{-1}\\ [-.5ex]{-2}\\ [-.5ex]{1}\end{bmatrix}$](img917.png) の直線である.
の直線である.
例 1.179 (平面と平面の交線)
連立方程式
で定まる直線を考える. この直線は 2 つの平面の共有点である. 第 2 式から第 1 式を引いて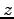 を消去すると
を消去すると
であり,第 1 式と第 2 式を足して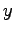 を消去すると
を消去すると
となる. これらより
を得る. 直線は点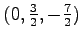 を通り,
方向ベクトル
を通り,
方向ベクトル
![$ \begin{bmatrix}{2}\\ [-.5ex]{-1}\\ [-.5ex]{3}\end{bmatrix}$](img923.png) の直線である.
また,パラメータ表示すると
の直線である.
また,パラメータ表示すると
である.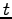 は任意であるから,
は任意であるから,
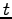 を
を
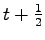 と置き換えると,
と置き換えると,
となり,式が簡単となる. このとき平面の方程式は
となる.直線は点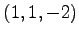 も通る.
も通る.
で定まる直線を考える. この直線は 2 つの平面の共有点である. 第 2 式から第 1 式を引いて
であり,第 1 式と第 2 式を足して
となる. これらより
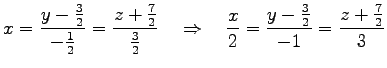 |
を得る. 直線は点
![$ \begin{bmatrix}{2}\\ [-.5ex]{-1}\\ [-.5ex]{3}\end{bmatrix}$](img923.png) の直線である.
また,パラメータ表示すると
の直線である.
また,パラメータ表示すると
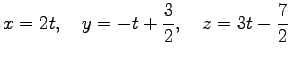 |
である.
となり,式が簡単となる. このとき平面の方程式は
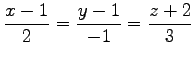 |
となる.直線は点
平成20年2月2日