1.31 外積を用いて平面の法線ベクトルを導出
注意 1.156 (
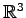 の平面の方程式)
の平面の方程式)
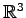 空間内の平面の方程式を考える.
まず,
空間内の平面の方程式を考える.
まず,
とおく.すると方程式
が成り立つ.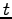 ,
, 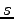 は任意のパラメータであるから消去して方程式とする.
第一式と第二式の
は任意のパラメータであるから消去して方程式とする.
第一式と第二式の 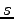 を消去し
を消去し 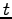 についてまとめると
についてまとめると
が得られる. 他の組合せでも同じ方程式を得る. この方程式は
とおくと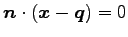 が成り立つ.
また,
が成り立つ.
また,
と表される. さらには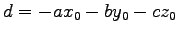 とおいて変形すれば
とおいて変形すれば
である. これらは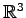 の平面の方程式の成分表示である.
ベクトル
の平面の方程式の成分表示である.
ベクトル 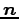 は
は
より,方向ベクトル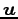 ,
, 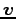 とそれぞれ直交する.
とそれぞれ直交する.
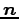 は法線ベクトルである.
また,
ベクトル
は法線ベクトルである.
また,
ベクトル 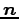 は
は
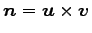 により与えられることに注意する.
により与えられることに注意する.
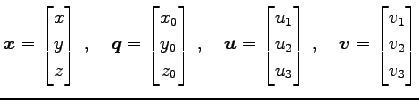 |
(196) |
とおく.すると方程式
| (197) |
が成り立つ.
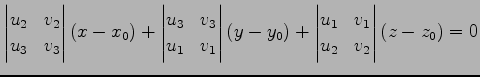 |
(198) |
が得られる. 他の組合せでも同じ方程式を得る. この方程式は
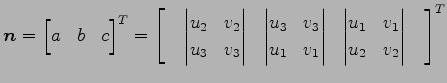 |
(199) |
とおくと
| (200) |
と表される. さらには
| (201) |
である. これらは
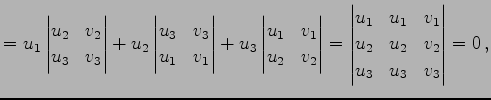 |
(202) | |
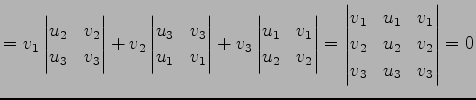 |
(203) |
より,方向ベクトル
例 1.157 (
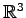 の平面の方程式の具体例)
点
の平面の方程式の具体例)
点 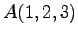 ,
, 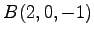 ,
,
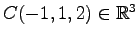 を
通る平面を考える.
点
を
通る平面を考える.
点
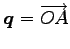 を通り
方向ベクトルが
を通り
方向ベクトルが
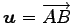 ,
,
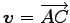 の平面と考える.
の平面と考える.
とする. このとき法線ベクトルは
である. 平面の方程式の成分表示は
より
であるから
を得る.また変形して
を得る.
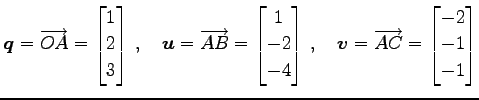 |
(204) |
とする. このとき法線ベクトルは
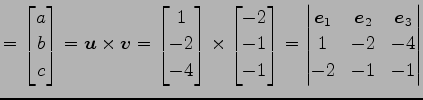 |
(205) | |
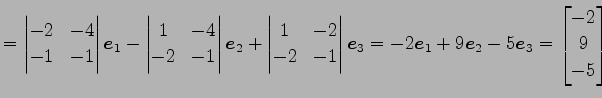 |
(206) |
である. 平面の方程式の成分表示は
| (207) |
より
| (208) |
であるから
| (209) |
を得る.また変形して
| (210) |
を得る.
例 1.158 (
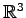 の平面の方程式の具体例)
3 点
の平面の方程式の具体例)
3 点 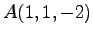 ,
, 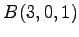 ,
, 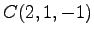 を通る
を通る
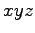 空間内の平面を考える.
法線ベクトルは
空間内の平面を考える.
法線ベクトルは
であり,点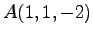 を通るので,
を通るので,
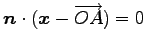 より
平面の方程式
より
平面の方程式
を得る.一般形で書けば
となる.さらに変形して
とする. 平面と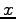 軸,
軸,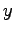 軸,
軸,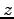 軸の交点はそれぞれ
軸の交点はそれぞれ
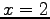 ,
, 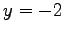 ,
, 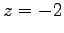 である.
である.
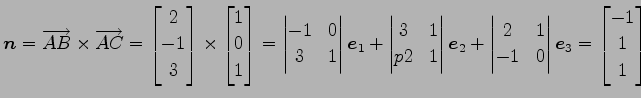 |
であり,点
を得る.一般形で書けば
となる.さらに変形して
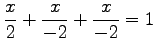 |
とする. 平面と
平成20年2月2日