Next: 4 行列式 Up: 3 連立一次方程式 Previous: 7 基本変形の行列表現 Contents
8 逆行列
定義 3.45 (逆行列)
行列 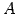 に対して
に対して
を満たす行列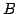 が存在するとき,
行列
が存在するとき,
行列 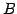 を行列
を行列 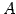 の逆行列(inverse matrix)と呼ぶ.
の逆行列(inverse matrix)と呼ぶ.
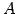 の逆行列は
の逆行列は 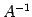 と表記する.
と表記する.
| (496) |
を満たす行列
問 3.46 (逆行列の性質)
逆行列をもつのは正方行列のみである.
これを示せ.
(証明)
![]() を満たす行列は可換な行列である.
可換な行列は正方行列のみである.
を満たす行列は可換な行列である.
可換な行列は正方行列のみである.
定理 3.47 (逆行列の一意性)
行列  が逆行列をもつとき,逆行列は一意に定まる.
が逆行列をもつとき,逆行列は一意に定まる.
となる.よって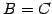 であり
であり 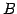 と
と  とは一致する.
とは一致する.
(証明)
![]() と
と ![]() が
が ![]() の逆行列であると仮定する.
このとき
の逆行列であると仮定する.
このとき ![]() ,
, ![]() が成り立つ.
これを用いて
が成り立つ.
これを用いて
| (497) |
となる.よって
定義 3.48 (行列の正則性)
正方行列 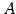 が逆行列をもつとき,
が逆行列をもつとき,
 は正則(regular)であるという.
正則な行列を正則行列(regular matrix)と呼ぶ.
は正則(regular)であるという.
正則な行列を正則行列(regular matrix)と呼ぶ.
定理 3.49 (逆行列をもつ十分条件)
正方行列  ,
, 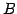 が
が 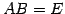 または
または 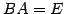 の
どちらか一方だけを満たすときでも
の
どちらか一方だけを満たすときでも
 は
は  の逆行列となる.
の逆行列となる.
(証明)
証明はずっとあとに行なう.
定理 3.50 (逆行列の計算法)
行列 ![$ [A\vert E]$](img1680.png) を簡約化して
を簡約化して ![$ [E\vert B]$](img1681.png) の形に変形できたとする.
このとき
の形に変形できたとする.
このとき  は
は 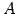 の逆行列
の逆行列 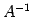 となる.
となる.
と書ける.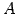 の左にかかっている行列をまとめて
の左にかかっている行列をまとめて 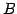 と書くと,
と書くと,
となる. を用いれば
を用いれば 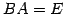 が成り立つ.
前述の定理より
が成り立つ.
前述の定理より 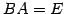 のとき
のとき 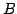 は
は 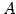 の逆行列
の逆行列 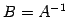 となる.
よって行列
となる.
よって行列  を求めればよい.
を求めればよい.
 は
は
と書ける. これはすなわち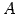 に行なった基本変形と同じ操作を
に行なった基本変形と同じ操作を  に
対して同じ順で行なうことを意味する.
これらの操作を同時に行なうには,
行列
に
対して同じ順で行なうことを意味する.
これらの操作を同時に行なうには,
行列 ![$ [A\vert E]$](img1703.png) に対して簡約化を行い
に対して簡約化を行い ![$ [E\vert B]$](img1704.png) の形にすればよい.
この一連の操作により
の形にすればよい.
この一連の操作により 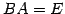 を得る.
を得る.
(証明)
行列 ![]() に基本変形
に基本変形 ![]() を繰り返し行ない
単位行列
を繰り返し行ない
単位行列 ![]() に変換されたとする.
このとき
に変換されたとする.
このとき
| (498) |
と書ける.
| (499) |
となる.
| (500) |
と書ける. これはすなわち
例 3.51 (逆行列の計算例)
行列
を考える.この行列の逆行列を求める. 行列![$ [A\,\vert\,E]$](img1708.png) に基本変形を次のように繰り返し行なう:
に基本変形を次のように繰り返し行なう:
よって, の逆行列
の逆行列
を得る.
 |
(501) |
を考える.この行列の逆行列を求める. 行列
![$\displaystyle = \left[ \begin{array}{ccc\vert ccc} 1 & 2 & 1 & 1 & 0 & 0 \\ 2 & 3 & 1 & 0 & 1 & 0 \\ 1 & 2 & 2 & 0 & 0 & 1 \end{array}\right]$](img1710.png) (一行目を (一行目を |
(502) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{ccc\vert ccc} 1 & 2 & 1 & 1 & 0 & 0 \\ 2 & 3 & 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & -1 & 0 & 1 \end{array}\right]$](img1712.png) (一行目を (一行目を |
(503) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{ccc\vert ccc} 1 & 2 & 1 & 1 & 0 & 0 \\ 0 & -1 & -1 & -2 & 1 & 0 \\ 0 & 0 & 1 & -1 & 0 & 1 \end{array}\right]$](img1714.png) (二行目を (二行目を |
(504) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{ccc\vert ccc} 1 & 0 & -1 & -3 & 2 & 0 \\ 0 & -1 & -1 & -2 & 1 & 0 \\ 0 & 0 & 1 & -1 & 0 & 1 \end{array}\right]$](img1716.png) (三行目を一行目に加える.) (三行目を一行目に加える.) |
(505) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{ccc\vert ccc} 1 & 0 & 0 & -4 & 2 & 1 \\ 0 & -1 & -1 & -2 & 1 & 0 \\ 0 & 0 & 1 & -1 & 0 & 1 \end{array}\right]$](img1717.png) (三行目を二行目に加える.) (三行目を二行目に加える.) |
(506) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{ccc\vert ccc} 1 & 0 & 0 & -4 & 2 & 1 \\ 0 & -1 & 0 & -3 & 1 & 1 \\ 0 & 0 & 1 & -1 & 0 & 1 \end{array}\right]$](img1718.png) (二行目を (二行目を |
(507) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{ccc\vert ccc} 1 & 0 & 0 & -4...
...& 3 & -1 &-1 \\ 0 & 0 & 1 & -1 & 0 & 1 \end{array}\right]=[E\,\vert\,A^{-1}]\,.$](img1720.png) |
(508) |
よって,
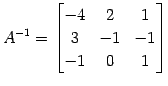 |
(509) |
を得る.
定理 3.52 (行列の正則性と緒性質)
正方行列 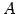 に対して次の(1)-(5) は同値である:
に対して次の(1)-(5) は同値である:
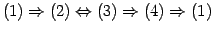 ,
,
 を示す.
を示す.
となる. は
は  の逆行列である.
よって
の逆行列である.
よって  は正則である.
は正則である.
- (1)
-
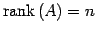 .
.
- (2)
 の簡約化は
の簡約化は  である.
である.
- (3)
- 任意の
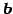 に対して
に対して
 は一意な解をもつ.
は一意な解をもつ.
- (4)
-
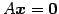 は自明な解
は自明な解
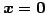 のみをもつ.
のみをもつ.
- (5)
 は正則である.
は正則である.
(証明)
![]() を示す.
を示す.
![]() は
は ![]() 型でフルランクであるから,
簡約化は明らかに
型でフルランクであるから,
簡約化は明らかに ![]() となる.
となる.
![]() を示す.
簡約化により
を示す.
簡約化により
![]() となるので,
方程式は
となるので,
方程式は
![]() となる.
よって解として一意な解
となる.
よって解として一意な解
![]() をもつ.
をもつ.
![]() を示す.
を示す.
![]() のとき
のとき
![]() であるから,
解として
であるから,
解として
![]() のみをもつ.
のみをもつ.
![]() を示す.
定理
を示す.
定理 ![]() より,
同次形方程式が自明な解のみをもつ必用十分条件は
より,
同次形方程式が自明な解のみをもつ必用十分条件は
![]() である.
である.
![]() を示す.
を示す.
![]() のときの解を
それぞれ
のときの解を
それぞれ
![]() とする.
このとき
とする.
このとき
| (510) | ||
| (511) | ||
| (512) |
となる.
![]() を示す.
を示す.
| (513) |
定理 3.53 (逆行列による解法)
正方行列 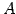 が正則なとき方程式
が正則なとき方程式
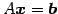 は
解
は
解
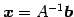 をもつ.
をもつ.
例 3.54 (逆行列をもたない具体例)
行列
の逆行列を考える. 例題![[*]](./icons/crossref.png) と同じように計算を行なう:
と同じように計算を行なう:
これより行列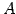 の簡約化は
の簡約化は
となる.よって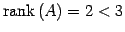 となる.
定理
となる.
定理 ![[*]](./icons/crossref.png) の
の
 より
より
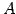 は正則ではない.
よって
は正則ではない.
よって 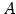 は逆行列をもたない.
は逆行列をもたない.
 |
(514) |
の逆行列を考える. 例題
![$\displaystyle = \left[ \begin{array}{ccc\vert ccc} 1 & 2 & 3 & 1 & 0 & 0 \\ 2 & 3 & 4 & 0 & 1 & 0 \\ 3 & 4 & 5 & 0 & 0 & 1 \end{array}\right]$](img1765.png) (一行目を (一行目を |
(515) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{ccc\vert ccc} 1 & 2 & 3 & 1 & 0 & 0 \\ 2 & 3 & 4 & 0 & 1 & 0 \\ 0 & -2 & -4 & -3 & 0 & 1 \end{array}\right]$](img1767.png) (一行目を (一行目を |
(516) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{ccc\vert ccc} 1 & 2 & 3 & 1 & 0 & 0 \\ 0 & -1 & -2 & -2 & 1 & 0 \\ 0 & -2 & -4 & -3 & 0 & 1 \end{array}\right]$](img1769.png) (二行目を (二行目を |
(517) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{ccc\vert ccc} 1 & 2 & 3 & 1 & 0 & 0 \\ 0 & 1 & 2 & 2 & -1 & 0 \\ 0 & -2 & -4 & -3 & 0 & 1 \end{array}\right]$](img1771.png) (二行目を (二行目を |
(518) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{ccc\vert ccc} 1 & 0 & -1 & -3 & 2 & 0 \\ 0 & 1 & 2 & 2 & -1 & 0 \\ 0 & -2 & -4 & -3 & 0 & 1 \end{array}\right]$](img1773.png) (二行目を (二行目を |
(519) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{ccc\vert ccc} 1 & 0 & -1 & -...
...2 & 0 \\ 0 & 1 & 2 & 2 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 1 \end{array}\right]\,.$](img1775.png) |
(520) |
これより行列
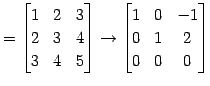 |
(521) |
となる.よって
例 3.55 (逆行列を用いた解法の具体例)
方程式
を考える. とすると
とすると
 より
解が求まる.
よって
より
解が求まる.
よって
を得る.
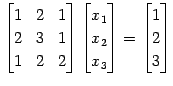 |
(522) |
を考える.
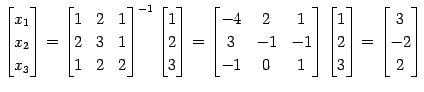 |
(523) |
を得る.
定理 3.56 (逆行列の性質)
正方行列  ,
,  が正則のとき次の関係式が成り立つ:
が正則のとき次の関係式が成り立つ:
- (1)
-
 .
.
- (2)
-
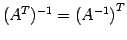 .
.
- (3)
-
 .
.
問 3.57
これを示せ.
(証明)
(3) を示す.
| (524) | ||
| (525) | ||
| (526) | ||
| (527) |
Next: 4 行列式 Up: 3 連立一次方程式 Previous: 7 基本変形の行列表現 Contents
Kondo Koichi

Created at 2004/11/26