Next: 8 逆行列 Up: 3 連立一次方程式 Previous: 6 ちょっとまとめ Contents
7 基本変形の行列表現
定理 3.40 (行列の積による行列の行の基本変形)
行列
![$ A=[a_{ij}]_{m\times n}$](img1535.png) が与えられたとき,
次に定義される行列
が与えられたとき,
次に定義される行列
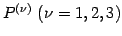 を左から掛けて,
積
を左から掛けて,
積
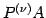 を考える.
このとき積
を考える.
このとき積
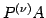 は行列の行の第
は行列の行の第 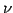 基本変形を
基本変形を
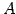 にほどこした行列と等しい.
にほどこした行列と等しい.
- (1)
- 第
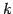 行を
行を 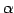 倍する.
倍する.
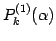
![$\displaystyle = \underset{k}{ \left[\begin{array}{ccc\vert c\vert ccc} \!1\! & ...
...[-.5ex] & & & & & \!\ddots\! & \\ [-.5ex] & & & & & & \!1\! \end{array}\right]}$](img1544.png)
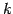
(448)
- (2)
- 第
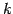 行と第
行と第 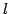 行を入れ替える.
行を入れ替える.
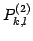
![$\displaystyle = \underset{k\qquad\qquad\,\,\,l}{ \left[\begin{array}{ccc\vert c...
...& & & & & & & \!\ddots\! & \\ [-.5ex] & & & & & & & & & & 1 \end{array}\right]}$](img1549.png)
(449)
- (3)
- 第
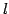 行を
行を 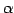 倍して第
倍して第 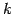 行に加える.
行に加える.
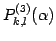
![$\displaystyle = \underset{k\qquad\qquad\,\,\,l}{ \left[\begin{array}{ccc\vert c...
...& & \!\ddots\! & \\ [-.5ex] & & & & & & & & & & 1 \end{array}\right]}\quad(k<l)$](img1554.png)
(450)
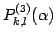
![$\displaystyle = \underset{l\qquad\qquad\,\,\,k}{ \left[\begin{array}{ccc\vert c...
...& & \!\ddots\! & \\ [-.5ex] & & & & & & & & & & 1 \end{array}\right]}\quad(l<k)$](img1556.png)
(451)
問 3.41
これを示せ.
例 3.42 (行列の行の基本変形の具体例)
行列
を考える. このとき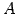 にいろいろな基本変形を行なうと次のようになる.
にいろいろな基本変形を行なうと次のようになる.
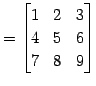 |
(452) |
を考える. このとき
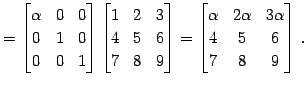 ← 第 ← 第 |
(453) | |
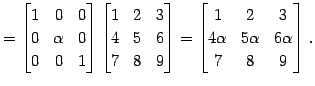 ← 第 ← 第 |
(454) | |
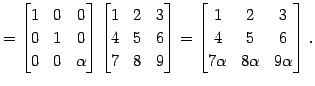 ← 第 ← 第 |
(455) | |
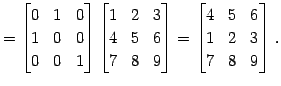 ← 第 ← 第 |
(456) | |
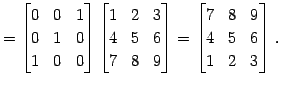 ← 第 ← 第 |
(457) | |
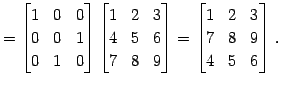 ← 第 ← 第 |
(458) | |
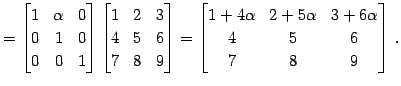 |
(459) | |
| ← 第 |
(460) | |
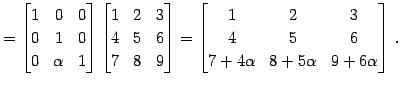 |
(461) | |
| ← 第 |
(462) | |
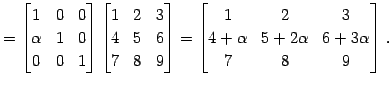 |
(463) | |
| ← 第 |
(464) |
例 3.43 (簡約化の行列表現)
行列 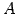 を簡約化し
を簡約化し 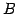 とする.
このとき
とする.
このとき
を満たす行列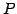 を求める.
簡約化を次のように行う:
を求める.
簡約化を次のように行う:
簡約化された行列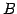 はここでは単位行列
はここでは単位行列 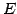 となる.
この結果を書き直すと
となる.
この結果を書き直すと
と書ける. ここで
とおいた. よって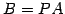 を満たす
を満たす 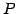 が得られる.
行列
が得られる.
行列 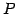 を具体的に求める.
を具体的に求める.
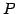 は
は 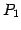 から
から 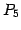 の積で
の積で
と表されるので, これを計算すれば良い. しかしながらこれは面倒である. 積の順番を
として計算する. これはすなわち, 単位行列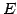 に対して
に対して
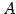 に行った基本変形と同じ操作を同じ順番で行うことを意味する.
よって
に行った基本変形と同じ操作を同じ順番で行うことを意味する.
よって
を得る. 以上より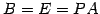 を満たす
を満たす
を求めた.
| (465) |
を満たす行列
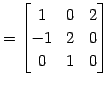 |
(466) | |
| (第一行目を第二行目に加える.) | (467) | |
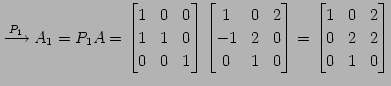 |
(468) | |
| (第三行目を |
(469) | |
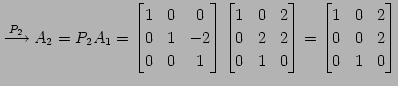 |
(470) | |
| (第二行目と第三行目を入れ替える.) | (471) | |
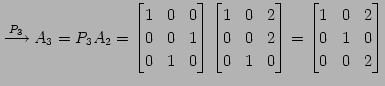 |
(472) | |
| (第三行目を |
(473) | |
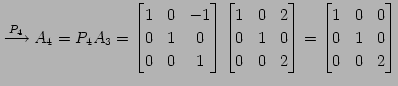 |
(474) | |
| (第三行目を |
(475) | |
 |
(476) |
簡約化された行列
| (477) | ||
| (478) |
と書ける. ここで
| (479) |
とおいた. よって
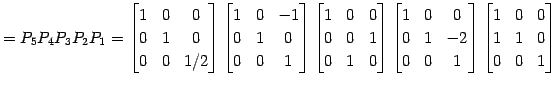 |
(480) |
と表されるので, これを計算すれば良い. しかしながらこれは面倒である. 積の順番を
| (481) |
として計算する. これはすなわち, 単位行列
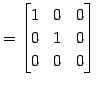 |
(482) | |
| (第一行目を第二行目に加える.) | (483) | |
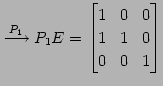 |
(484) | |
| (第三行目を |
(485) | |
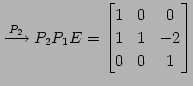 |
(486) | |
| (第二行目と第三行目を入れ替える.) | (487) | |
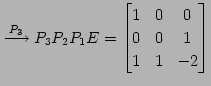 |
(488) | |
| (第三行目を |
(489) | |
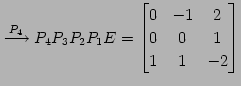 |
(490) | |
| (第三行目を |
(491) | |
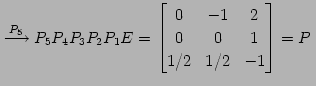 |
(492) |
を得る. 以上より
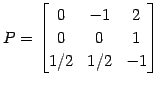 |
(493) |
を求めた.
注意 3.44 (変換の行列表現)
行列 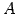 から行列
から行列 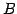 への変換を
への変換を 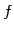 とする.
すなわち
とする.
すなわち
とする.関数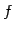 は入力が行列で出力も行列である.
いま簡約化を表す関数
は入力が行列で出力も行列である.
いま簡約化を表す関数 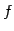 を考える.
このとき
を考える.
このとき
と表される. 関数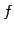 は入力行列
は入力行列 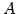 に対して
左から
に対して
左から 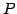 を掛ける操作を意味する.
簡約化という操作は行列
を掛ける操作を意味する.
簡約化という操作は行列 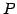 と対応する.
行列の変換においては
入力,出力,操作ともに全て行列で表される.
と対応する.
行列の変換においては
入力,出力,操作ともに全て行列で表される.
| (494) |
とする.関数
| (495) |
と表される. 関数
Next: 8 逆行列 Up: 3 連立一次方程式 Previous: 6 ちょっとまとめ Contents
Kondo Koichi

Created at 2004/11/26