Next: 6 ちょっとまとめ Up: 3 連立一次方程式 Previous: 4 行列の簡約化 Contents
5 連立一次方程式の解法
例 3.26 (任意定数を含む解の具体例)
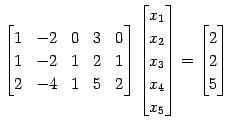
方程式
を考える. 拡大係数行列の簡約化を行なうと,
を得る. ここで
が成立することに注意する. 簡約化された拡大係数行列より方程式を復元すると,
である. 主成分の列と同じ位置にある変数を左辺に残し, 他の項を右辺に移項すると
となる. 右辺にある変数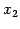 ,
, 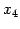 は独立に任意の値をとる.
よって
は独立に任意の値をとる.
よって
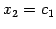 ,
,
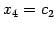 とおけば,解として
とおけば,解として
を得る. 解は 5 次元平面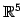 内の
ある 2 次元平面となる.
内の
ある 2 次元平面となる.
 |
(397) |
を考える. 拡大係数行列の簡約化を行なうと,
![$\displaystyle \left[\begin{array}{ccccc\vert c} 1 & -2 & 0 & 3 & 0 & 2 \\ 1 & -...
... & 0 & 2 \\ 0 & 0 & 1 & -1 & 0 & -1 \\ 0 & 0 & 0 & 0 & 1 & 1 \end{array}\right]$](img1405.png) |
(398) |
を得る. ここで
| (399) |
が成立することに注意する. 簡約化された拡大係数行列より方程式を復元すると,
![$\displaystyle \left\{\begin{array}{cccccl} x_{1} & -2x_{2} & & +3x_{4} & & = 2 ...
...m] & & x_{3} & -x_{4} & & = -1 \\ [.5em] & & & & x_{5} & = 1 \end{array}\right.$](img1407.png) |
(400) |
である. 主成分の列と同じ位置にある変数を左辺に残し, 他の項を右辺に移項すると
![$\displaystyle \left\{\begin{array}{cl} x_{1} & = 2 + 2x_{2} - 3x_{4} \\ [.5em] x_{3} & = -1 +x_{4} \\ [.5em] x_{5} & = 1 \end{array}\right.$](img1408.png) |
(401) |
となる. 右辺にある変数
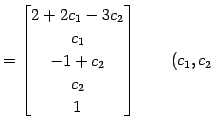 :任意定数 :任意定数 |
(402) | |
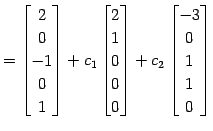 |
(403) |
を得る. 解は 5 次元平面
例 3.27 (解が存在しない具体例)
方程式
を考える. 拡大係数行列の簡約化を行なうと,
を得る. 方程式に書き戻すと
となる. 最後の行は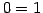 となるから,
どのような
となるから,
どのような 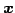 をとっても成立することはない.
よってこの連立方程式の解は存在しない.
ここで
をとっても成立することはない.
よってこの連立方程式の解は存在しない.
ここで
が成り立つことに注意する. このとき解をもたない.
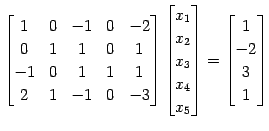 |
(404) |
を考える. 拡大係数行列の簡約化を行なうと,
![$\displaystyle = \left[ \begin{array}{ccccc\vert c} 1 & 0 & -1 & 0 & -2 & 1 \\ 0...
...0 \\ 0 & 0 & 0 & 1 & -1 & 0 \\ \hline 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right]$](img1420.png) |
(405) |
を得る. 方程式に書き戻すと
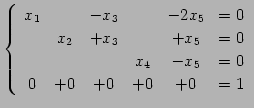 |
(406) |
となる. 最後の行は
| (407) |
が成り立つことに注意する. このとき解をもたない.
連立一次方程式
| (408) |
を考える. 以後この方程式に対して議論する.
方程式
![]() の解を求めるには
まず,拡大係数行列
の解を求めるには
まず,拡大係数行列
![]() の簡約化を行なう.
このとき得られた行列が
の簡約化を行なう.
このとき得られた行列が
![$\displaystyle [A\vert\vec{b}] \overset{\text{簡約化}}{\longrightarrow} \left[\b...
... & & &&& \cdots & 0 & 0 \\ 0 & \cdots & & &&& \cdots & 0 & 0 \end{array}\right]$](img1428.png) |
(409) |
と得られたとしよう. このとき零ベクトルではない一番下の行に着目すると
| (410) |
となる.
![$\displaystyle A \overset{\text{簡約化}}{\longrightarrow} \left[\begin{array}{cc...
...& \cdots & & &&& \cdots & 0 \\ 0 & \cdots & & &&& \cdots & 0 \end{array}\right]$](img1432.png) |
(411) |
であるから,
| (412) |
が成り立つ. この条件のもとでは解をもたない. 次に簡約化の結果として
![$\displaystyle = \left[\begin{array}{cccccccc\vert c} \!1\! & ** & \!0\! & ** & ...
... & & &&& \cdots & 0 & 0 \\ 0 & \cdots & & &&& \cdots & 0 & 0 \end{array}\right]$](img1435.png) |
(413) |
を得たとする. こときは解をもつ. 係数行列のランクは
定理 3.28 (連立一次方程式の可解条件)
方程式
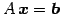 が解をもつための
必要十分条件は
が解をもつための
必要十分条件は
である.
| (414) |
である.
解に任意定数を含まないのは, 簡約行列のすべての列に主成分が現れるときである. つまり係数行列のランクと変数の個数が一致するときである. これをまとめると以下の定理を得る.
定理 3.29 (一意な解をもつ条件)
方程式
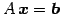 が唯一つの解をもつための
必用十分条件は
が唯一つの解をもつための
必用十分条件は
である.
| (415) |
である.
定理 3.30 (任意定数を含む解をもつ条件)
方程式
は
のとき任意定数を含む解をもつ. このとき任意定数の個数は
である.
| (416) |
は
| (417) |
のとき任意定数を含む解をもつ. このとき任意定数の個数は
| (418) |
である.
定義 3.31 (同次形方程式)
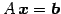 において
において 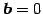 が成り立つとき,
方程式
が成り立つとき,
方程式
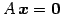 は同次形(homogeneous)と呼ぶ.
は同次形(homogeneous)と呼ぶ.
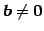 とき非同次形(inhomogeneous)と呼ぶ.
とき非同次形(inhomogeneous)と呼ぶ.
定理 3.32 (同次形の解の存在)
同次方程式は
![$ \mathrm{rank}\,(A)=\mathrm{rank}\,[A\vert\vec{0}]$](img1448.png) が常になり立つので,
常に解
が常になり立つので,
常に解
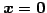 をもつ.
をもつ.
定義 3.33 (同次形の自明解)
同次方程式
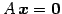 の解
の解
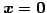 を
自明な解と呼ぶ.
を
自明な解と呼ぶ.
定理 3.34 (同次方程式の解)
同次方程式
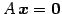 について次の条件が成り立つ:
について次の条件が成り立つ:
である. 拡大係数行列の一番右の列の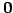 はランクに影響を与えない.
よって定理の条件を得る.
はランクに影響を与えない.
よって定理の条件を得る.
を得る.(1)の定理より自明でない解をもつ. 証明終了.
- (1)
- 自明な解
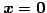 のみをもつための必用十分条件は
のみをもつための必用十分条件は
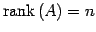
(419)
である. - (2)
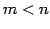 のとき,方程式は自明でない解(任意定数を含む解)をもつ.
のとき,方程式は自明でない解(任意定数を含む解)をもつ.
(証明)(1)前述の定理より唯一つの解をもつための必要十分条件は
| (420) |
である. 拡大係数行列の一番右の列の
(2)
![]() ,
,
![]() と条件
と条件 ![]() より
より
| (421) |
を得る.(1)の定理より自明でない解をもつ. 証明終了.
例 3.35 (同次形方程式の解)
方程式
を考える. 係数行列を簡約化して
を得る.よって解は
となる. 解は原点を通る2次元平面である.
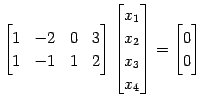 |
(422) |
を考える. 係数行列を簡約化して
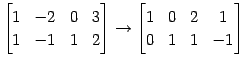 |
(423) |
を得る.よって解は
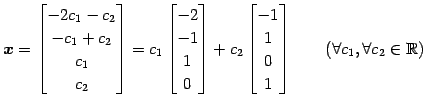 |
(424) |
となる. 解は原点を通る2次元平面である.
Next: 6 ちょっとまとめ Up: 3 連立一次方程式 Previous: 4 行列の簡約化 Contents
Kondo Koichi

Created at 2004/11/26