Next: 5 連立一次方程式の解法 Up: 3 連立一次方程式 Previous: 3 連立一次方程式の基本変形 Contents
4 行列の簡約化
連立一次方程式
| (367) | ||
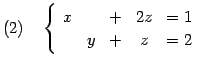 |
(368) |
を考えよる. これらの方程式は 解が一意には定まらない例である. このような方程式の解を具体的に求める.
方程式(1)を変形すると
| (369) |
である. この式より
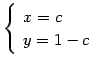 |
(370) |
を得る. ただし
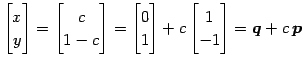 |
(371) |
と書ける. よって解全体がなす集合は点
方程式(2)の解を求める. 方程式を書き直すと
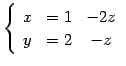 |
(372) |
となる. 左辺には
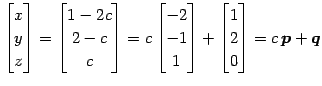 |
(373) |
を得る. 解全体の集合は 3 次元空間
拡大係数行列はそれぞれ
![$\displaystyle (1)\quad [A\,\vert\,\vec{b}]= \left[ \begin{array}{cc\vert c} 1 &...
...ft[ \begin{array}{ccc\vert c} 1 & 0 & 2 & 1 \\ 0 & 1 & 1 & 2 \end{array}\right]$](img1364.png) |
(374) |
となる. もっと一般には次のような行列を考える.
定義 3.15 (階段行列)
行列が
という形をしているとき, この行列を簡約な行列または 階段行列と呼ぶ. また, 各行の一番左の 0 ではない成分を主成分と呼ぶ.
![$\displaystyle \left[\begin{array}{cccccccc} \!1\! & ** & \!0\! & ** & \!0\! & *...
... \\ \vdots& & & & & & &\vdots\\ 0 &\cdots& & & & &\cdots & 0 \end{array}\right]$](img1365.png) |
(375) |
という形をしているとき, この行列を簡約な行列または 階段行列と呼ぶ. また, 各行の一番左の 0 ではない成分を主成分と呼ぶ.
例 3.16 (簡約な行列の具体例)
次の行列は簡約な行列である:
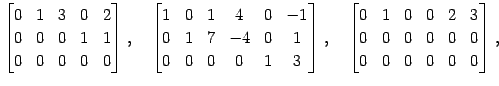 |
(376) | |
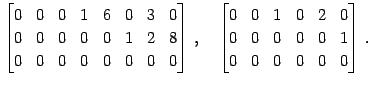 |
(377) |
定義 3.17 (簡約化)
行列 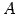 に基本変形を繰り返し,
簡約な行列
に基本変形を繰り返し,
簡約な行列 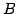 を得ることを簡約化と呼ぶ.
を得ることを簡約化と呼ぶ.
例 3.18 (簡約化の計算例)
簡約化の具体的な計算例を示す:
(1)
(2)
(3)
(4)
(1)
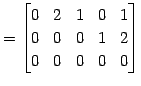 |
(378) | |
| (第一行目を |
(379) | |
 |
(380) |
(2)
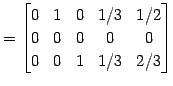 |
(381) | |
| (第二行目と第三行目を入れ替える.) | (382) | |
 |
(383) |
(3)
 |
(384) | |
| (第二行目を |
(385) | |
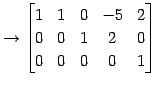 |
(386) | |
| (第三行目を |
(387) | |
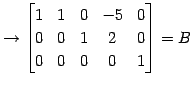 |
(388) |
(4)
 |
(389) | |
| (第一行目を第三行目を入れ替える.) | (390) | |
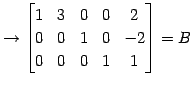 |
(391) |
定理 3.19 (簡約化の一意性)
任意の行列は基本変形により一意に簡約化できる.
定義 3.20 (行列の階数)
行列 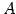 を簡約化した行列を
を簡約化した行列を 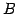 とする.
このとき
行列
とする.
このとき
行列 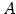 に対する行列の階数(rank)を
に対する行列の階数(rank)を
と定義する.
| (392) |
と定義する.
例 3.21 (階数の具体例)
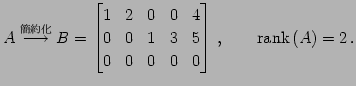 |
(393) |
定理 3.23 (階数に関する定理)
行列 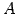 が
が 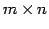 型のとき,
型のとき,
が成り立つ.
| (396) |
が成り立つ.
問 3.24
これを示せ.
問 3.25
教科書(p.27)問題2.2.
Next: 5 連立一次方程式の解法 Up: 3 連立一次方程式 Previous: 3 連立一次方程式の基本変形 Contents
Kondo Koichi

Created at 2004/11/26