Next: 4 行列の簡約化 Up: 3 連立一次方程式 Previous: 2 ベクトルの一次結合と連立一次方程式 Contents
3 連立一次方程式の基本変形
定義 3.8 (連立一次方程式の基本変形)
連立一次方程式に対する次のの操作を
連立一次方程式の基本変形と呼ぶ.
- (1)
- 一つの式を
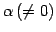 倍する.
倍する.
- (2)
- 二つの式を入れ替える.
- (3)
- 一つの式を
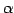 倍して別の行に加える.
倍して別の行に加える.
連立一次方程式に基本変形をして得られた方程式と 元の方程式とは等価な方程式である. すなわち両者は同じ解をもつ.
連立一次方程式とその行列表現は,方程式としては等価なものである. 連立一次方程式の基本変形は, 行列表現では次の行列の行の基本変形となる.
定義 3.9 (行列の行の基本変形)
行列に対する次の操作を
行列の行の基本変形
(matrix elementary row transformation)と呼ぶ.
- (1)
- 一つの行を
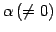 倍する.
倍する.
- (2)
- 二つの行を入れ替える.
- (3)
- 一つの行を
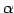 倍して別の行に加える.
倍して別の行に加える.
定理 3.10 (掃き出し法)
拡大係数行列
![$ [A\vert\vec{b}]$](img1303.png) に基本変形を繰り返し行ない,
に基本変形を繰り返し行ない,
の形に変形ができたとする. このとき解は
と得られる. この解法を 掃き出し法(sweeping-out method)または ガウスの消去法(Gaussian elimination)と呼ぶ.
![$\displaystyle [A\vert\vec{b}] \to \left[ \begin{array}{cccc\vert c} 1 & & &\sma...
...& & \vdots \\ \smash{\text{\huge$0$}}&& & 1 & \tilde{b}_{m} \end{array} \right]$](img1304.png) |
(344) |
の形に変形ができたとする. このとき解は
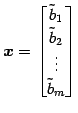 |
(345) |
と得られる. この解法を 掃き出し法(sweeping-out method)または ガウスの消去法(Gaussian elimination)と呼ぶ.
例 3.11 (掃き出し法による計算例)
連立一次方程式
を考える. 基本変形を繰り返し行なう. 連立方程式とその拡大係数行列
に基本変形をほどこす. 第二式を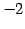 倍し第一式に加えると
倍し第一式に加えると
を得る. 第一式と第二式を入れ換えて
となる.第二式を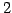 倍し第一式に加えると
倍し第一式に加えると
となる.第二式を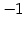 倍すると
倍すると
を得る.結局拡大係数行列は
と変形された. 以上より,解は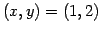 と求まる.
と求まる.
![$\displaystyle \left\{ \begin{array}{cccc} 2x & + & 3y & =8 \\ [1ex] x & + & 2y & =5 \end{array}\right.$](img1306.png) |
(346) |
を考える. 基本変形を繰り返し行なう. 連立方程式とその拡大係数行列
![$\displaystyle \left\{ \begin{array}{cccc} 2x & + & 3y & =8 \\ [1ex] x & + & 2y ...
...\qquad \left[\begin{array}{cc\vert c} 2 & 3 & 8 \\ 1 & 2 & 5 \end{array}\right]$](img1307.png) |
(347) |
に基本変形をほどこす. 第二式を
![$\displaystyle \left\{ \begin{array}{cccc} & & -y & =-2 \\ [1ex] x & + & 2y & =5...
...quad \left[\begin{array}{cc\vert c} 0 & -1 & -2 \\ 1 & 2 & 5 \end{array}\right]$](img1309.png) |
(348) |
を得る. 第一式と第二式を入れ換えて
![$\displaystyle \left\{ \begin{array}{cccc} x & + & 2y & =5 \\ [1ex] & & -y & =-2...
...quad \left[\begin{array}{cc\vert c} 1 & 2 & 5 \\ 0 & -1 & -2 \end{array}\right]$](img1310.png) |
(349) |
となる.第二式を
![$\displaystyle \left\{ \begin{array}{cccc} x & & & =1 \\ [1ex] & & -y & =-2 \end...
...quad \left[\begin{array}{cc\vert c} 1 & 0 & 1 \\ 0 & -1 & -2 \end{array}\right]$](img1312.png) |
(350) |
となる.第二式を
![$\displaystyle \left\{ \begin{array}{cccc} x & & & =1 \\ [1ex] & & y & =2 \end{a...
...\qquad \left[\begin{array}{cc\vert c} 1 & 0 & 1 \\ 0 & 1 & 2 \end{array}\right]$](img1314.png) |
(351) |
を得る.結局拡大係数行列は
![$\displaystyle \left[\begin{array}{cc\vert c} 2 & 3 & 8 \\ 1 & 2 & 5 \end{array}...
...t] \to \left[\begin{array}{cc\vert c} 1 & 0 & 1 \\ 0 & 1 & 2 \end{array}\right]$](img1315.png) |
(352) |
と変形された. 以上より,解は
例 3.12 (掃き出し法による計算例)
連立一次方程式
を考える. 拡大係数行列に基本変形を繰り返し行なう. 連立一次方程式とその拡大係数行列
に基本変形をほどこす. 第三行を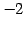 倍して第一式に足すと
倍して第一式に足すと
となる. 第三行を第一式に足すと
となる. 第一式と第三行を入れ替えると
となる. 第三式を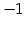 倍して第一行に加えると
倍して第一行に加えると
となる. 第三式を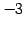 倍して第二行に加えると
倍して第二行に加えると
となる. 第二式と第三式を入れ替えると
となる. 第三式を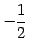 倍すると
倍すると
となる. 第三式を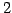 倍して第一式に足すと
倍して第一式に足すと
となる. 第三式を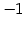 倍して第二式に足すと
倍して第二式に足すと
となる. よって
を得る. 以上より,解は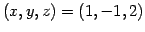 と求まる.
と求まる.
![$\displaystyle \left\{ \begin{array}{cccccc} 2x & + & 3y & - & z & =-3 \\ [.5ex] -x & + & 2y & + & 2z & =1 \\ [.5ex] x & + & y & - & z & =-2 \end{array}\right.$](img1317.png) |
(353) |
を考える. 拡大係数行列に基本変形を繰り返し行なう. 連立一次方程式とその拡大係数行列
![$\displaystyle \left\{ \begin{array}{cccccc} 2x & + & 3y & - & z & =-3 \\ [.5ex]...
...vert c} 2 & 3 & -1 & -3 \\ -1 & 2 & 2 & 1 \\ 1 & 1 & -1 & -2 \end{array}\right]$](img1318.png) |
(354) |
に基本変形をほどこす. 第三行を
![$\displaystyle \left\{ \begin{array}{cccccc} & & y & + & z & =1 \\ [.5ex] -x & +...
...c\vert c} 0 & 1 & 1 & 1 \\ -1 & 2 & 2 & 1 \\ 1 & 1 & -1 & -2 \end{array}\right]$](img1320.png) |
(355) |
となる. 第三行を第一式に足すと
![$\displaystyle \left\{ \begin{array}{cccccc} & & y & + & z & =1 \\ [.5ex] & & 3y...
...c\vert c} 0 & 1 & 1 & 1 \\ 0 & 3 & 1 & -1 \\ 1 & 1 & -1 & -2 \end{array}\right]$](img1321.png) |
(356) |
となる. 第一式と第三行を入れ替えると
![$\displaystyle \left\{ \begin{array}{cccccc} x & + & y & - & z & =-2 \\ [.5ex] &...
...c\vert c} 1 & 1 & -1 & -2 \\ 0 & 3 & 1 & -1 \\ 0 & 1 & 1 & 1 \end{array}\right]$](img1322.png) |
(357) |
となる. 第三式を
![$\displaystyle \left\{ \begin{array}{cccccc} x & & & - & 2z & =-3 \\ [.5ex] & & ...
...c\vert c} 1 & 0 & -2 & -3 \\ 0 & 3 & 1 & -1 \\ 0 & 1 & 1 & 1 \end{array}\right]$](img1324.png) |
(358) |
となる. 第三式を
![$\displaystyle \left\{ \begin{array}{cccccc} x & & & - & 2z & =-3 \\ [.5ex] & & ...
...\vert c} 1 & 0 & -2 & -3 \\ 0 & 0 & -2 & -4 \\ 0 & 1 & 1 & 1 \end{array}\right]$](img1326.png) |
(359) |
となる. 第二式と第三式を入れ替えると
![$\displaystyle \left\{ \begin{array}{cccccc} x & & & - & 2z & =-3 \\ [.5ex] & & ...
...\vert c} 1 & 0 & -2 & -3 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & -2 & -4 \end{array}\right]$](img1327.png) |
(360) |
となる. 第三式を
![$\displaystyle \left\{ \begin{array}{cccccc} x & & & - & 2z & =-3 \\ [.5ex] & & ...
...cc\vert c} 1 & 0 & -2 & -3 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 2 \end{array}\right]$](img1329.png) |
(361) |
となる. 第三式を
![$\displaystyle \left\{ \begin{array}{cccccc} x & & & & & =1 \\ [.5ex] & & y & + ...
...{ccc\vert c} 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 2 \end{array}\right]$](img1331.png) |
(362) |
となる. 第三式を
![$\displaystyle \left\{ \begin{array}{cccccc} x & & & & & =1 \\ [.5ex] & & y & & ...
...ccc\vert c} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 2 \end{array}\right]$](img1333.png) |
(363) |
となる. よって
![$\displaystyle \left[\begin{array}{ccc\vert c} 2 & 3 & -1 & -3 \\ -1 & 2 & 2 & 1...
...ccc\vert c} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 2 \end{array}\right]$](img1334.png) |
(364) |
を得る. 以上より,解は
例 3.13 (掃き出し法による計算例)
連立一次方程式
を考える. 拡大係数行列に基本変形を繰り返し行ない,
を得る. 以上より,解は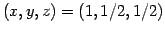 と求まる.
と求まる.
![$\displaystyle \left\{ \begin{array}{cccccc} x & + & y & - & z & =1 \\ [.5ex] 2x & + & y & + & 3z & =4 \\ [.5ex] -x & + & 2y& - & 4z & =-2 \end{array}\right.$](img1336.png) |
(365) |
を考える. 拡大係数行列に基本変形を繰り返し行ない,
![$\displaystyle \left[\begin{array}{ccc\vert c} 1 & 1 & -1 & 1 \\ 2 & 1 & 3 & 4 \...
...\vert c} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1/2 \\ 0 & 0 & 1 & 1/2 \end{array}\right]$](img1337.png) |
(366) |
を得る. 以上より,解は
問 3.14
教科書(p.22)問題2.1.
Next: 4 行列の簡約化 Up: 3 連立一次方程式 Previous: 2 ベクトルの一次結合と連立一次方程式 Contents
Kondo Koichi

Created at 2004/11/26