3.6 演習問題 〜 多重積分,累次積分,積分の順序の交換
問 3.34 (累次積分)
下図の領域 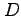 は
(i)
は
(i) 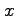 に関する単純な領域,
(ii)
に関する単純な領域,
(ii) 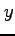 に関する単純な領域とみることができる.
(i), (ii) の場合それぞれにおいて次の多重積分を計算せよ.
に関する単純な領域とみることができる.
(i), (ii) の場合それぞれにおいて次の多重積分を計算せよ.
(1)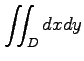 (2)
(2)
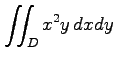
![\includegraphics[width=.25\textwidth]{sekibun-D1.eps}](img2066.png)
(1)
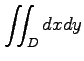 (2)
(2)
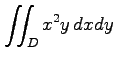
![\includegraphics[width=.25\textwidth]{sekibun-D1.eps}](img2066.png)
問 3.35 (累次積分)
次の多重積分を計算せよ.
(1)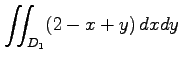 (2)
(2)
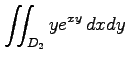 (3)
(3)
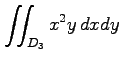 (4)
(4)
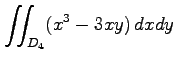
(1)
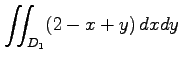 (2)
(2)
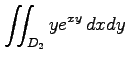 (3)
(3)
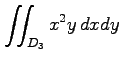 (4)
(4)
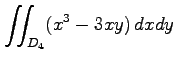
![\includegraphics[width=.25\textwidth]{enshu/D_1.eps}](img2071.png) |
![\includegraphics[width=.25\textwidth]{enshu/D_2.eps}](img2072.png) |
![\includegraphics[width=.25\textwidth]{enshu/hcir.eps}](img2073.png) |
![\includegraphics[width=.25\textwidth]{enshu/D_4.eps}](img2074.png)
|
問 3.36 (累次積分)
積分領域を図示し,多重積分を計算せよ.
(1)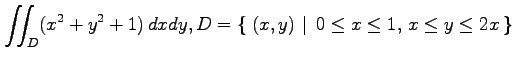
(2)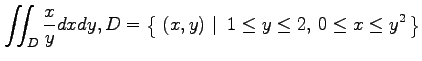
(3)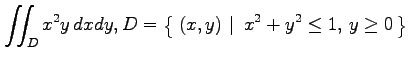
(4)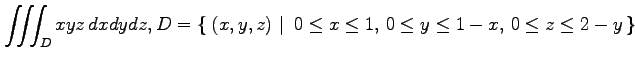
(5)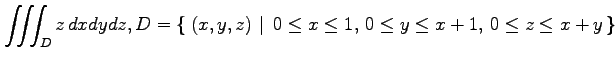
(6)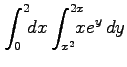 (7)
(7)
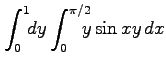
(8)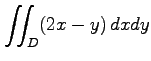 ,
,
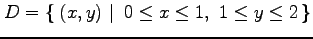
(9)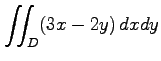 ,
,
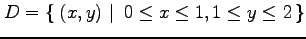
(10)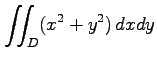 ,
,
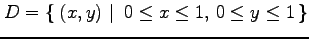
(11)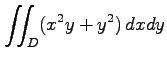 ,
,
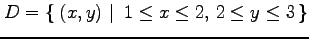
(12)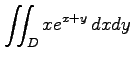 ,
,
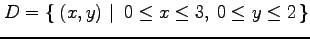
(13)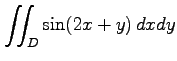 ,
,
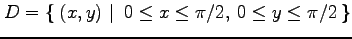
(14)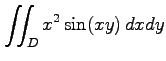 ,
,
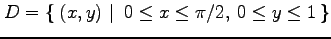
(15)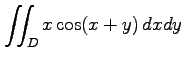 ,
,
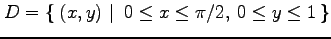
(16)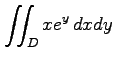 ,
,
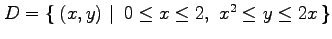
(17)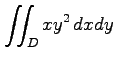 ,
,
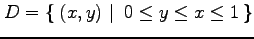
(18)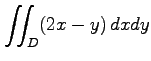 ,
,
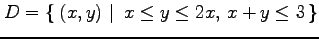
(19)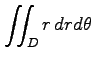 ,
,
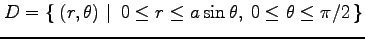
(20)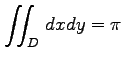 ,
,
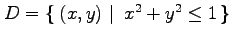 となることを示せ.
となることを示せ.
(21)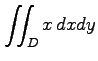 ,
,
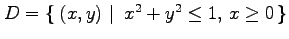
(22)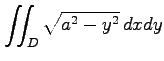 ,
,
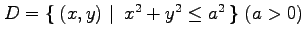
(23)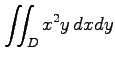 ,
,
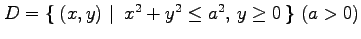
(24)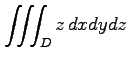 ,
,
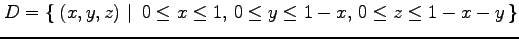
(25)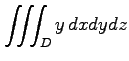 ,
,
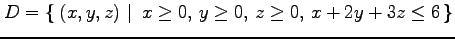
(26)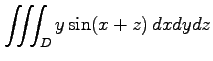 ,
,
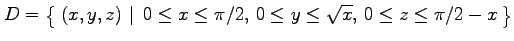
(27)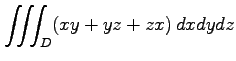 ,
,
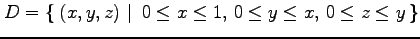
(28)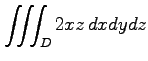 ,
,
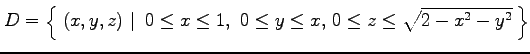
(1)
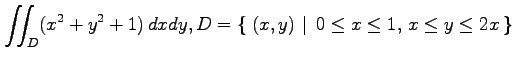
(2)
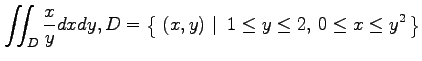
(3)
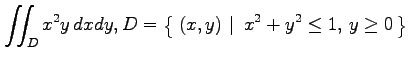
(4)
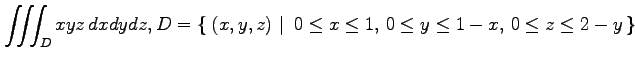
(5)
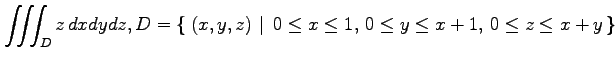
(6)
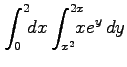 (7)
(7)
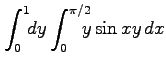
(8)
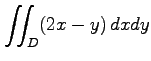 ,
,
(9)
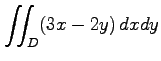 ,
,
(10)
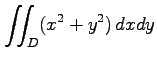 ,
,
(11)
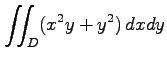 ,
,
(12)
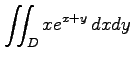 ,
,
(13)
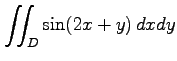 ,
,
(14)
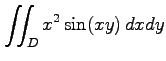 ,
,
(15)
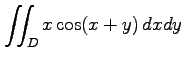 ,
,
(16)
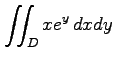 ,
,
(17)
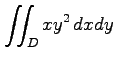 ,
,
(18)
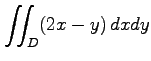 ,
,
(19)
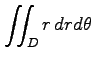 ,
,
(20)
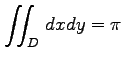 ,
,
(21)
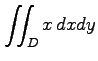 ,
,
(22)
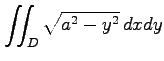 ,
,
(23)
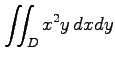 ,
,
(24)
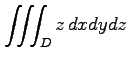 ,
,
(25)
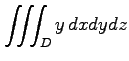 ,
,
(26)
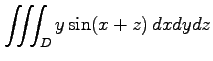 ,
,
(27)
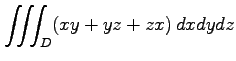 ,
,
(28)
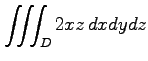 ,
,
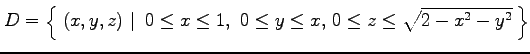
問 3.37 (積分の順序の交換)
 を埋めて次の式を完成させよ.
ただし
を埋めて次の式を完成させよ.
ただし  は上記の図の領域とする.
は上記の図の領域とする.
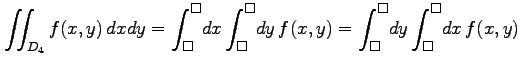 |
問 3.38 (積分の順序の交換)
次の積分の領域を図示し,積分の順序を変更せよ.
(1)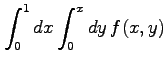 (2)
(2)
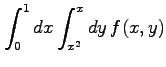 (3)
(3)
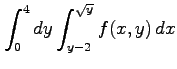
(4)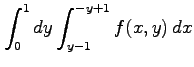 (5)
(5)
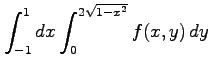 (6)
(6)
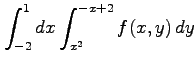
(7)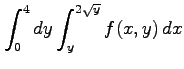
(1)
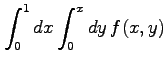 (2)
(2)
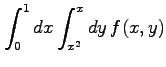 (3)
(3)
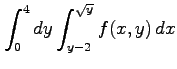
(4)
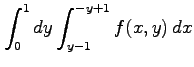 (5)
(5)
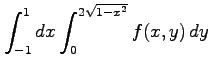 (6)
(6)
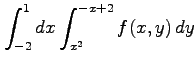
(7)
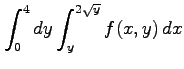
平成21年1月14日