3.7 長方形領域における積分
定理 3.39 (長方形領域における多重積分)
領域 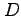 が長方形領域
が長方形領域
のとき,
が成り立つ.
のとき,
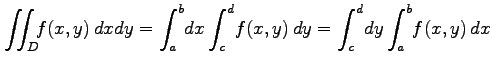 |
が成り立つ.
注意 3.40 (長方形領域における多重積分)
長方形領域であれば 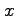 と
と 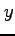 の積分の順が
交換可能である.
の積分の順が
交換可能である.
例 3.41 (長方形領域における多重積分)
多重積分
を求める.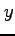 ,
, 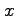 の順で積分すると
の順で積分すると
となる. 逆に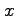 ,
, 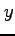 の順で積分すると
の順で積分すると
となる. 積分の順を入れ替えても結果は同じである.
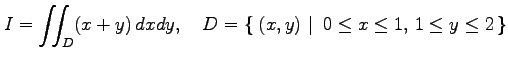 |
を求める.
![$\displaystyle = \int_0^1dx\int_1^2(x+y)dy= \int_0^1dx\left[\vrule height1.5em w...
...t1.5em width0em depth0.1em\,{\frac{x^2}{2}+\frac{3x}{2}}\,\right]_{x=0}^{x=1}=2$](img2133.png) |
となる. 逆に
![$\displaystyle = \int_1^2dy\int_0^1(x+y)dx= \int_1^2dy\left[\vrule height1.5em w...
...ht1.5em width0em depth0.1em\,{\frac{y}{2}+\frac{y^2}{2}}\,\right]_{y=1}^{y=2}=2$](img2134.png) |
となる. 積分の順を入れ替えても結果は同じである.
問 3.42 (長方形領域における多重積分)
多重積分
を求めよ.
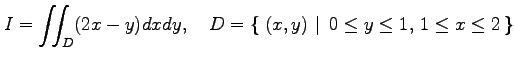 |
を求めよ.
定理 3.43 (長方形領域における多重積分)
領域 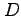 が長方形領域
が長方形領域
であり,被積分関数が変数分離型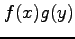 のとき,
のとき,
が成り立つ.
であり,被積分関数が変数分離型
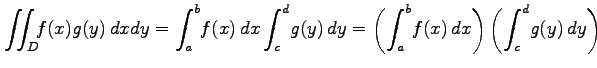 |
が成り立つ.
例 3.44 (長方形領域における多重積分)
多重積分
を求める.長方形領域で被積分関数は変数分離型であるから,
となる.
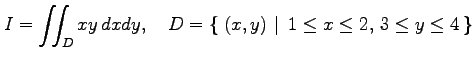 |
を求める.長方形領域で被積分関数は変数分離型であるから,
![$\displaystyle =\int_1^2x\,dx\int_3^4y\,dy= \left(\int_1^2x\,dx\right)\left(\int...
...ft[\vrule height1.5em width0em depth0.1em\,{\frac{y^2}{2}}\,\right]_{y=3}^{y=4}$](img2139.png) |
||
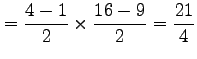 |
となる.
平成21年1月14日