4.11 余因子
定義 4.73 (小部分行列と余因子)
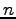 次正方行列
次正方行列
![$ A=[a_{ij}]_{n\times n}$](img2139.png) の
第
の
第 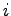 行と第
行と第 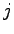 列を取り除いた
列を取り除いた 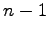 次の小行列を
次の小行列を
と書く. このとき行列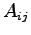 の行列式
の行列式
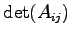 に符合をつけた数
に符合をつけた数
を における
における 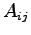 の余因子(cofactor)と呼ぶ.
の余因子(cofactor)と呼ぶ.
![$\displaystyle A_{ij}= \left[ \begin{array}{ccc\vert ccc} a_{1,1} & \cdots & a_{...
...n,1} & \cdots & a_{n,j-1} & a_{n,j+1} & \cdots & a_{n,n} \\ \end{array} \right]$](img2140.png) |
(731) |
と書く. このとき行列
| (732) |
を
例 4.74 (余因子の具体例)
行列
を考える. このとき小行列
より,余因子は
である.
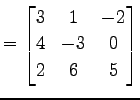 |
(733) |
を考える. このとき小行列
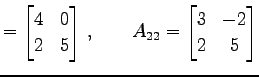 |
(734) |
より,余因子は
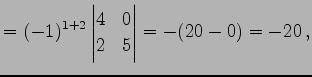 |
(735) | |
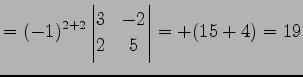 |
(736) |
である.
平成20年2月2日