4.10 ちょっとまとめ

定理 4.71 (行列式の性質)    

(1)

一つの行を 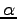$\alpha$ 倍すると行列式は 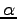$\alpha$ 倍となる．

(2)

一つの行が二つの行ベクトルの和で表せる行列式は， 他の行はそのままで， その行に各々の行ベクトルをとった行列式の和に等しい．

(3)

二つの行を入れ替えると行列式は 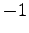$-1$ 倍となる．

(4)

二つの行が等しい行列式は 0 である．

(5)

一つの行を 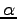$\alpha$ 倍して別の行に加えても 行列式は変らない．

定理 4.72 (行列式の性質)    

(1)

一つの列を 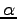$\alpha$ 倍すると行列式は 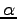$\alpha$ 倍となる．

(2)

一つの列が二つの列ベクトルの和で表せる行列式は， 他の列はそのままで， その列に各々の列ベクトルをとった行列式の和に等しい．

(3)

二つの列を入れ替えると行列式は 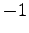$-1$ 倍となる．

(4)

二つの列が等しい行列式は 0 である．

(5)

一つの列を 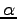$\alpha$ 倍して別の列に加えても 行列式は変らない．

（証明） $\det({A}^{T})=\det(A)$ より， $\det({A}^{T})$ に対する行の基本変形は， $\det(A)$ に対する列の基本変形と等しい．

平成20年2月2日