4.9 行列の正則性と行列式
定理 4.67 (行列の正則性と行列式)
行列  が正則行列のとき
が正則行列のとき
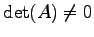 が成り立つ.
が成り立つ.
問 4.68
これを示せ.
が成立する. 各辺の行列式をとると
であるから
を得る. よって
が成り立つ.
(証明)
![]() は逆行列をもつので,
は逆行列をもつので,
| (724) |
が成立する. 各辺の行列式をとると
| (725) | ||
| (726) | ||
| (727) |
であるから
| (728) |
を得る. よって
| (729) |
が成り立つ.
定理 4.69 (逆行列の行列式)
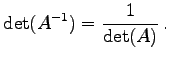 |
(730) |
問 4.70 (逆行列の行列式)
これを示せ.
(証明)
前の定理の証明の
![]() より示される.
より示される.
平成20年2月2日