4.8 行列式の性質

定理 4.62 (行列式の性質)  

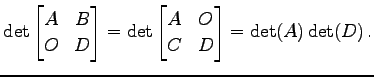$$\det \begin{bmatrix}A & B \\ O & D \end{bmatrix} = \det \begin{bmatrix}A & O \\ C & D \end{bmatrix} = \det(A)\det(D)\,.$$ (717)

例 4.63 (行列式の計算例)  

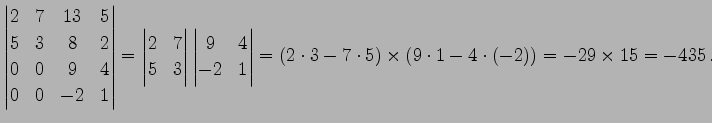$$\begin{vmatrix}2 & 7 & 13 & 5 \\ 5 & 3 & 8 & 2 \\ 0 & 0 & 9 & 4 \... ...d{vmatrix} = (2\cdot3-7\cdot5)\times (9\cdot1-4\cdot(-2))= -29\times 15=-435\,.$$ (718)

定理 4.64 (行列の積の行列式)  

$$\det(AB)=\det(A)\det(B)\,.$$ (719)

注意 4.65 (行列の積の行列式) 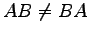  $AB\neq BA$ のときでさえも

$$\det(AB)=\det(BA)$$ (720)

が成り立つことに注意する． これは

$$\det(AB) =\det(A)\cdot\det(B)=\det(B)\cdot\det(A)=\det(BA)$$ (721)

より示される．

問 4.66 (行列式の性質の使用例)  

$$(a^2+b^2)(c^2+d^2)= (ac-bd)^2+(ad+bc)^2$$ (722)

が成り立つことを

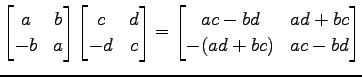$$\begin{bmatrix}a & b \\ -b & a \end{bmatrix} \begin{bmatrix}c & d... ... \end{bmatrix} = \begin{bmatrix}ac-bd & ad+bc \\ -(ad+bc) & ac-bd \end{bmatrix}$$ (723)

の両辺の行列式をとることで示せ．

平成20年2月2日