3.15 演習問題 〜 基本変形の行列表現
問 3.56 (行の基本変形)
次の関係式をみたす行列 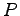 を求めよ.
を求めよ.
(1)![$ \begin{bmatrix}
2\! & \!3\! & \!-1 \\ [-0.5ex] 2\! & \!0\! & \!-8
\end{bmatrix}=P\begin{bmatrix}
2\! & \!3\! & \!-1 \\ [-0.5ex] -1\! & \!0\! & \!4
\end{bmatrix}$](img1760.png) (2)
(2)
![$ \begin{bmatrix}
3\! & \!0\! & \!-1 \\ [-0.5ex] -6\! & \!3\! & \!-9 \\ [-0.5ex]...
... \!-1 \\ [-0.5ex] 2\! & \!-1\! & \!3 \\ [-0.5ex] -4\! &
5\! & \!0
\end{bmatrix}$](img1761.png)
(3)![$ \begin{bmatrix}
0\! & \!3 \\ [-0.5ex] -2\! & \!3 \\ [-0.5ex] 2\! & \!1 \\ [-0....
... [-0.5ex] 4\! & \!-1 \\ [-0.5ex] 2\! & \!1 \\ [-0.5ex] -2\! & \!3
\end{bmatrix}$](img1762.png) (4)
(4)
![$ \begin{bmatrix}
6\! & \!1\! & \!0 \\ [-0.5ex] 2\! & \!-1\! & \!2 \\ [-0.5ex] -...
...& \!0 \\ [-0.5ex] -3\! & \!0\! & \!4 \\ [-0.5ex] 2\! &
-1\! & \!2
\end{bmatrix}$](img1763.png)
(5)![$ \begin{bmatrix}
1\! & \!3\! & \!2 \\ [-0.5ex] 0\! & \!4\! & \!-1 \\ [-0.5ex] 1...
... & \!2 \\ [-0.5ex] 0\! & \!4\! & \!-1 \\ [-0.5ex] 3\! &
2\! & \!4
\end{bmatrix}$](img1764.png) (6)
(6)
![$ \begin{bmatrix}
1\! & \!-4\! & \!5 \\ [-0.5ex] 2\! & \!3\! & \!-1 \\ [-0.5ex] ...
...& \!2 \\ [-0.5ex] 2\! & \!3\! & \!-1 \\ [-0.5ex] 1\! &
-3\! & \!3
\end{bmatrix}$](img1765.png)
(1)
![$ \begin{bmatrix}
2\! & \!3\! & \!-1 \\ [-0.5ex] 2\! & \!0\! & \!-8
\end{bmatrix}=P\begin{bmatrix}
2\! & \!3\! & \!-1 \\ [-0.5ex] -1\! & \!0\! & \!4
\end{bmatrix}$](img1760.png) (2)
(2)
![$ \begin{bmatrix}
3\! & \!0\! & \!-1 \\ [-0.5ex] -6\! & \!3\! & \!-9 \\ [-0.5ex]...
... \!-1 \\ [-0.5ex] 2\! & \!-1\! & \!3 \\ [-0.5ex] -4\! &
5\! & \!0
\end{bmatrix}$](img1761.png)
(3)
![$ \begin{bmatrix}
0\! & \!3 \\ [-0.5ex] -2\! & \!3 \\ [-0.5ex] 2\! & \!1 \\ [-0....
... [-0.5ex] 4\! & \!-1 \\ [-0.5ex] 2\! & \!1 \\ [-0.5ex] -2\! & \!3
\end{bmatrix}$](img1762.png) (4)
(4)
![$ \begin{bmatrix}
6\! & \!1\! & \!0 \\ [-0.5ex] 2\! & \!-1\! & \!2 \\ [-0.5ex] -...
...& \!0 \\ [-0.5ex] -3\! & \!0\! & \!4 \\ [-0.5ex] 2\! &
-1\! & \!2
\end{bmatrix}$](img1763.png)
(5)
![$ \begin{bmatrix}
1\! & \!3\! & \!2 \\ [-0.5ex] 0\! & \!4\! & \!-1 \\ [-0.5ex] 1...
... & \!2 \\ [-0.5ex] 0\! & \!4\! & \!-1 \\ [-0.5ex] 3\! &
2\! & \!4
\end{bmatrix}$](img1764.png) (6)
(6)
![$ \begin{bmatrix}
1\! & \!-4\! & \!5 \\ [-0.5ex] 2\! & \!3\! & \!-1 \\ [-0.5ex] ...
...& \!2 \\ [-0.5ex] 2\! & \!3\! & \!-1 \\ [-0.5ex] 1\! &
-3\! & \!3
\end{bmatrix}$](img1765.png)
問 3.57 (列の基本変形)
次の関係式をみたす行列 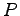 を求めよ.
を求めよ.
(1)![$ \begin{bmatrix}
2\! & \!2\! & \!0 \\ [-0.5ex] 3\! & \!0\! & \!1 \\ [-0.5ex] -4...
...& \!0 \\ [-0.5ex] 3\! & \!0\! & \!1 \\ [-0.5ex] -4\! &
2\! & \!1
\end{bmatrix}P$](img1766.png) (2)
(2)
![$ \begin{bmatrix}
2\! & \!3\! & \!-1\! & \!0 \\ [-0.5ex] -1\! & \!0\! & \!-2\! &...
...! & \!0\! & \!-1\! & \!3 \\ [-0.5ex] -1\! & \!4\! & \!-2\! & \!0
\end{bmatrix}P$](img1767.png)
(3)![$ \begin{bmatrix}
0\! & \!3\! & \!-1 \\ [-0.5ex] -3\! & \!4\! & \!2 \\ [-0.5ex] ...
...& \!3 \\ [-0.5ex] -3\! & \!2\! & \!4 \\ [-0.5ex] 6\! &
0\! & \!1
\end{bmatrix}P$](img1768.png) (4)
(4)
![$ \begin{bmatrix}
1\! & \!-2\! & \!2 \\ [-0.5ex] 2\! & \!3\! & \!5 \\ [-0.5ex] -...
... \!0 \\ [-0.5ex] 2\! & \!3\! & \!1 \\ [-0.5ex] -4\! &
-1\! & \!3
\end{bmatrix}P$](img1769.png)
(1)
![$ \begin{bmatrix}
2\! & \!2\! & \!0 \\ [-0.5ex] 3\! & \!0\! & \!1 \\ [-0.5ex] -4...
...& \!0 \\ [-0.5ex] 3\! & \!0\! & \!1 \\ [-0.5ex] -4\! &
2\! & \!1
\end{bmatrix}P$](img1766.png) (2)
(2)
![$ \begin{bmatrix}
2\! & \!3\! & \!-1\! & \!0 \\ [-0.5ex] -1\! & \!0\! & \!-2\! &...
...! & \!0\! & \!-1\! & \!3 \\ [-0.5ex] -1\! & \!4\! & \!-2\! & \!0
\end{bmatrix}P$](img1767.png)
(3)
![$ \begin{bmatrix}
0\! & \!3\! & \!-1 \\ [-0.5ex] -3\! & \!4\! & \!2 \\ [-0.5ex] ...
...& \!3 \\ [-0.5ex] -3\! & \!2\! & \!4 \\ [-0.5ex] 6\! &
0\! & \!1
\end{bmatrix}P$](img1768.png) (4)
(4)
![$ \begin{bmatrix}
1\! & \!-2\! & \!2 \\ [-0.5ex] 2\! & \!3\! & \!5 \\ [-0.5ex] -...
... \!0 \\ [-0.5ex] 2\! & \!3\! & \!1 \\ [-0.5ex] -4\! &
-1\! & \!3
\end{bmatrix}P$](img1769.png)
問 3.58 (簡約化の行列表現)
行列  を簡約化し
を簡約化し  とする.このとき
とする.このとき 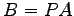 をみたす行列
をみたす行列 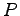 を求めよ.
を求めよ.
(1)![$ A=
\begin{bmatrix}
1\! & \!4\! & \!3 \\ [-0.5ex] 2\! & \!8\! & \!6
\end{bmatrix}$](img1770.png) (2)
(2)
![$ A=
\begin{bmatrix}
1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!3\! & \!1
\end{bmatrix}$](img1771.png) (3)
(3)
![$ A=
\begin{bmatrix}
2\! & \!-2\! & \!0\! & \!3 \\ [-0.5ex] 1\! & \!-1\! & \!1\! & \!2
\end{bmatrix}$](img1772.png) (4)
(4)
![$ A=
\begin{bmatrix}
2\! & \!1 \\ [-0.5ex] 3\! & \!-7 \\ [-0.5ex] -6\! & \!1 \\ [-0.5ex] 5\! & \!-8
\end{bmatrix}$](img1773.png)
(5)![$ A=
\begin{bmatrix}
1\! & \!0\! & \!2 \\ [-0.5ex] -1\! & \!2\! & \!0 \\ [-0.5ex] 0\! & \!1\!
& \!0
\end{bmatrix}$](img1774.png) (6)
(6)
![$ A=
\begin{bmatrix}
1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!3\! & \!3 \\ [-0.5ex] -1\! & \!1\!
& \!4
\end{bmatrix}$](img1775.png) (7)
(7)
![$ A=
\begin{bmatrix}
1\! & \!0\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!1\! & \!1\! & \!0
\\ [-0.5ex] 0\! & \!1\! & \!1\! & \!0
\end{bmatrix}$](img1776.png) (8)
(8)
![$ A=
\begin{bmatrix}
0\! & \!1\! & \!2\! & \!1 \\ [-0.5ex] 0\! & \!0\! & \!2\! & \!0
\\ [-0.5ex] 1\! & \!0\! & \!0\! & \!3
\end{bmatrix}$](img1777.png)
(1)
![$ A=
\begin{bmatrix}
1\! & \!4\! & \!3 \\ [-0.5ex] 2\! & \!8\! & \!6
\end{bmatrix}$](img1770.png) (2)
(2)
![$ A=
\begin{bmatrix}
1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!3\! & \!1
\end{bmatrix}$](img1771.png) (3)
(3)
![$ A=
\begin{bmatrix}
2\! & \!-2\! & \!0\! & \!3 \\ [-0.5ex] 1\! & \!-1\! & \!1\! & \!2
\end{bmatrix}$](img1772.png) (4)
(4)
![$ A=
\begin{bmatrix}
2\! & \!1 \\ [-0.5ex] 3\! & \!-7 \\ [-0.5ex] -6\! & \!1 \\ [-0.5ex] 5\! & \!-8
\end{bmatrix}$](img1773.png)
(5)
![$ A=
\begin{bmatrix}
1\! & \!0\! & \!2 \\ [-0.5ex] -1\! & \!2\! & \!0 \\ [-0.5ex] 0\! & \!1\!
& \!0
\end{bmatrix}$](img1774.png) (6)
(6)
![$ A=
\begin{bmatrix}
1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!3\! & \!3 \\ [-0.5ex] -1\! & \!1\!
& \!4
\end{bmatrix}$](img1775.png) (7)
(7)
![$ A=
\begin{bmatrix}
1\! & \!0\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!1\! & \!1\! & \!0
\\ [-0.5ex] 0\! & \!1\! & \!1\! & \!0
\end{bmatrix}$](img1776.png) (8)
(8)
![$ A=
\begin{bmatrix}
0\! & \!1\! & \!2\! & \!1 \\ [-0.5ex] 0\! & \!0\! & \!2\! & \!0
\\ [-0.5ex] 1\! & \!0\! & \!0\! & \!3
\end{bmatrix}$](img1777.png)
平成20年2月2日