3.13 演習問題 〜 行列の簡約化,階数
問 3.49 (階数)
次の行列の階数を求めよ.
ただし,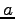 は実数とする.
は実数とする.
(1)![$ \begin{bmatrix}
2\! & \!-1 \\ [-0.5ex] -4\! & \!2
\end{bmatrix}$](img1619.png) (2)
(2)
![$ \begin{bmatrix}
1\! & \!4\! & \!3 \\ [-0.5ex] 2\! & \!8\! & \!6
\end{bmatrix}$](img1620.png) (3)
(3)
![$ \begin{bmatrix}
1\! & \!3 \\ [-0.5ex] 0\! & \!-2 \\ [-0.5ex] 5\! & \!-1 \\ [-0.5ex]
-2\! & \!3
\end{bmatrix}$](img1621.png) (4)
(4)
![$ \begin{bmatrix}
2\! & \!1 \\ [-0.5ex] 3\! & \!-7 \\ [-0.5ex] -6\! & \!1 \\ [-0.5ex]
5\! & \!-8
\end{bmatrix}$](img1622.png) (5)
(5)
![$ \begin{bmatrix}
-1\! & \!3\! & \!0 \\ [-0.5ex] 2\! & \!1\! & \!-3 \\ [-0.5ex] 4\! &
-5\! & \!-3
\end{bmatrix}$](img1623.png)
(6)![$ \begin{bmatrix}
0\! & \!2\! & \!3 \\ [-0.5ex] 0\! & \!4\! & \!6 \\ [-0.5ex] 0\! &
6\! & \!9
\end{bmatrix}$](img1624.png) (7)
(7)
![$ \begin{bmatrix}
1\! & \!2\! & \!3 \\ [-0.5ex] 2\! & \!1\! & \!3 \\ [-0.5ex] 3\! &
2\! & \!1
\end{bmatrix}$](img1625.png) (8)
(8)
![$ \begin{bmatrix}
1\! & \!3\! & \!4 \\ [-0.5ex] 8\! & \!1\! & \!9 \\ [-0.5ex] 4\! &
2\! & \!6
\end{bmatrix}$](img1626.png) (9)
(9)
![$ \begin{bmatrix}
1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!3\! & \!3 \\ [-0.5ex] -1\! &
1\! & \!4
\end{bmatrix}$](img1627.png) (10)
(10)
![$ \begin{bmatrix}
1\! & \!2\! & \!-1 \\ [-0.5ex] 2\! & \!-1\! & \!3 \\ [-0.5ex] 4\! &
3\! & \!1
\end{bmatrix}$](img1628.png)
(11)![$ \begin{bmatrix}
2\! & \!-1\! & \!1 \\ [-0.5ex] 4\! & \!-2\! & \!2 \\ [-0.5ex] -6\! &
3\! & \!-3
\end{bmatrix}$](img1629.png) (12)
(12)
![$ \begin{bmatrix}
1\! & \!1\! & \!2 \\ [-0.5ex] 4\! & \!5\! & \!5 \\ [-0.5ex] 5\! &
8\! & \!1 \\ [-0.5ex] -1\! & \!-2\! & \!2
\end{bmatrix}$](img1630.png) (13)
(13)
![$ \begin{bmatrix}
1\! & \!2\! & \!-3 \\ [-0.5ex] 2\! & \!1\! & \!0 \\ [-0.5ex] -2\! &
-1\! & \!3 \\ [-0.5ex] -1\! & \!4\! & \!-2
\end{bmatrix}$](img1631.png) (14)
(14)
![$ \begin{bmatrix}
0\! & \!1\! & \!1\! & \!3 \\ [-0.5ex] 1\! & \!2\! & \!3\! & \!2
\\ [-0.5ex] 2\! & \!3\! & \!5\! & \!1
\end{bmatrix}$](img1632.png)
(15)![$ \begin{bmatrix}
1\! & \!2\! & \!3\! & \!4 \\ [-0.5ex] 1\! & \!2\! & \!4\! & \!5
\\ [-0.5ex] 2\! & \!4\! & \!5\! & \!7
\end{bmatrix}$](img1633.png) (16)
(16)
![$ \begin{bmatrix}
1\! & \!2\! & \!5\! & \!9 \\ [-0.5ex] 1\! & \!1\! & \!2\! & \!5
\\ [-0.5ex] 3\! & \!2\! & \!3\! & \!11
\end{bmatrix}$](img1634.png) (17)
(17)
![$ \begin{bmatrix}
2\! & \!2\! & \!4\! & \!0 \\ [-0.5ex] 4\! & \!5\! & \!11\! & \!1
\\ [-0.5ex] -7\! & \!-9\! & \!-20\! & \!2
\end{bmatrix}$](img1635.png) (18)
(18)
![$ \begin{bmatrix}
0\! & \!1\! & \!0\! & \!1 \\ [-0.5ex] -1\! & \!0\! & \!1\! & \...
... 0\! & \!-1\! & \!0\! & \!1 \\ [-0.5ex] -1\! & \!0\! &
-1\! & \!0
\end{bmatrix}$](img1636.png)
(19)![$ \begin{bmatrix}
1\! & \!1\! & \!-2\! & \!1\! & \!3 \\ [-0.5ex] 2\! & \!-1\! & ...
...!
& \!2\! & \!6 \\ [-0.5ex] 3\! & \!2\! & \!-4\! & \!-3\! & \!-9
\end{bmatrix}$](img1637.png) (20)
(20)
![$ \begin{bmatrix}
1\! & \!1\! & \!-1\! & \!1\! & \!1 \\ [-0.5ex] -3\! & \!-1\! &...
...
& \!-1\! & \!0 \\ [-0.5ex] 11\! & \!5\! & \!-5\! & \!a\! & \!a+2
\end{bmatrix}$](img1638.png) (21)
(21)
![$ \begin{bmatrix}
1\! & \!1\! & \!2\! & \!-3\! & \!4 \\ [-0.5ex] 0\! & \!2\! & \...
...4\! & \!-5\! & \!8
\\ [-0.5ex] 1\! & \!3\! & \!5\! & \!-7\! & \!9
\end{bmatrix}$](img1639.png)
(22)![$ \begin{bmatrix}
1\! & \!3\! & \!1\! & \!-2\! & \!-3 \\ [-0.5ex] 1\! & \!4\! & ...
...! & \!-7\! & \!-3
\\ [-0.5ex] 3\! & \!8\! & \!1\! & \!-7\! & \!-8
\end{bmatrix}$](img1640.png) (23)
(23)
![$ \begin{bmatrix}
1\! & \!3\! & \!-2\! & \!5\! & \!4 \\ [-0.5ex] 1\! & \!4\! & \...
...2\! & \!4\! & \!3 \\ [-0.5ex]
2\! & \!7\! & \!-3\! & \!6\! & \!13
\end{bmatrix}$](img1641.png) (24)
(24)
![$ \begin{bmatrix}
1\! & \!2\! & \!-3\! & \!-2\! & \!-3 \\ [-0.5ex] 1\! & \!3\! &...
... & \!-2\! &
-11 \\ [-0.5ex] 2\! & \!1\! & \!-9\! & \!-10\! & \!-3
\end{bmatrix}$](img1642.png)
(25)![$ \begin{bmatrix}
1\! & \!3\! & \!1\! & \!-3\! & \!2 \\ [-0.5ex] 1\! & \!3\! & \...
...\!-2\! & \!1\! & \!3 \\ [-0.5ex] 1\! &
2\! & \!2\! & \!-3\! & \!2
\end{bmatrix}$](img1643.png) (26)
(26)
![$ \begin{bmatrix}
1\! & \!4\! & \!-2\! & \!4\! & \!-5\! & \!4\! & \!1 \\ [-0.5ex...
...5 \\ [-0.5ex] 3\! &
10\! & \!-1\! & \!-9\! & \!6\! & \!8\! & \!-2
\end{bmatrix}$](img1644.png)
(1)
![$ \begin{bmatrix}
2\! & \!-1 \\ [-0.5ex] -4\! & \!2
\end{bmatrix}$](img1619.png) (2)
(2)
![$ \begin{bmatrix}
1\! & \!4\! & \!3 \\ [-0.5ex] 2\! & \!8\! & \!6
\end{bmatrix}$](img1620.png) (3)
(3)
![$ \begin{bmatrix}
1\! & \!3 \\ [-0.5ex] 0\! & \!-2 \\ [-0.5ex] 5\! & \!-1 \\ [-0.5ex]
-2\! & \!3
\end{bmatrix}$](img1621.png) (4)
(4)
![$ \begin{bmatrix}
2\! & \!1 \\ [-0.5ex] 3\! & \!-7 \\ [-0.5ex] -6\! & \!1 \\ [-0.5ex]
5\! & \!-8
\end{bmatrix}$](img1622.png) (5)
(5)
![$ \begin{bmatrix}
-1\! & \!3\! & \!0 \\ [-0.5ex] 2\! & \!1\! & \!-3 \\ [-0.5ex] 4\! &
-5\! & \!-3
\end{bmatrix}$](img1623.png)
(6)
![$ \begin{bmatrix}
0\! & \!2\! & \!3 \\ [-0.5ex] 0\! & \!4\! & \!6 \\ [-0.5ex] 0\! &
6\! & \!9
\end{bmatrix}$](img1624.png) (7)
(7)
![$ \begin{bmatrix}
1\! & \!2\! & \!3 \\ [-0.5ex] 2\! & \!1\! & \!3 \\ [-0.5ex] 3\! &
2\! & \!1
\end{bmatrix}$](img1625.png) (8)
(8)
![$ \begin{bmatrix}
1\! & \!3\! & \!4 \\ [-0.5ex] 8\! & \!1\! & \!9 \\ [-0.5ex] 4\! &
2\! & \!6
\end{bmatrix}$](img1626.png) (9)
(9)
![$ \begin{bmatrix}
1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!3\! & \!3 \\ [-0.5ex] -1\! &
1\! & \!4
\end{bmatrix}$](img1627.png) (10)
(10)
![$ \begin{bmatrix}
1\! & \!2\! & \!-1 \\ [-0.5ex] 2\! & \!-1\! & \!3 \\ [-0.5ex] 4\! &
3\! & \!1
\end{bmatrix}$](img1628.png)
(11)
![$ \begin{bmatrix}
2\! & \!-1\! & \!1 \\ [-0.5ex] 4\! & \!-2\! & \!2 \\ [-0.5ex] -6\! &
3\! & \!-3
\end{bmatrix}$](img1629.png) (12)
(12)
![$ \begin{bmatrix}
1\! & \!1\! & \!2 \\ [-0.5ex] 4\! & \!5\! & \!5 \\ [-0.5ex] 5\! &
8\! & \!1 \\ [-0.5ex] -1\! & \!-2\! & \!2
\end{bmatrix}$](img1630.png) (13)
(13)
![$ \begin{bmatrix}
1\! & \!2\! & \!-3 \\ [-0.5ex] 2\! & \!1\! & \!0 \\ [-0.5ex] -2\! &
-1\! & \!3 \\ [-0.5ex] -1\! & \!4\! & \!-2
\end{bmatrix}$](img1631.png) (14)
(14)
![$ \begin{bmatrix}
0\! & \!1\! & \!1\! & \!3 \\ [-0.5ex] 1\! & \!2\! & \!3\! & \!2
\\ [-0.5ex] 2\! & \!3\! & \!5\! & \!1
\end{bmatrix}$](img1632.png)
(15)
![$ \begin{bmatrix}
1\! & \!2\! & \!3\! & \!4 \\ [-0.5ex] 1\! & \!2\! & \!4\! & \!5
\\ [-0.5ex] 2\! & \!4\! & \!5\! & \!7
\end{bmatrix}$](img1633.png) (16)
(16)
![$ \begin{bmatrix}
1\! & \!2\! & \!5\! & \!9 \\ [-0.5ex] 1\! & \!1\! & \!2\! & \!5
\\ [-0.5ex] 3\! & \!2\! & \!3\! & \!11
\end{bmatrix}$](img1634.png) (17)
(17)
![$ \begin{bmatrix}
2\! & \!2\! & \!4\! & \!0 \\ [-0.5ex] 4\! & \!5\! & \!11\! & \!1
\\ [-0.5ex] -7\! & \!-9\! & \!-20\! & \!2
\end{bmatrix}$](img1635.png) (18)
(18)
![$ \begin{bmatrix}
0\! & \!1\! & \!0\! & \!1 \\ [-0.5ex] -1\! & \!0\! & \!1\! & \...
... 0\! & \!-1\! & \!0\! & \!1 \\ [-0.5ex] -1\! & \!0\! &
-1\! & \!0
\end{bmatrix}$](img1636.png)
(19)
![$ \begin{bmatrix}
1\! & \!1\! & \!-2\! & \!1\! & \!3 \\ [-0.5ex] 2\! & \!-1\! & ...
...!
& \!2\! & \!6 \\ [-0.5ex] 3\! & \!2\! & \!-4\! & \!-3\! & \!-9
\end{bmatrix}$](img1637.png) (20)
(20)
![$ \begin{bmatrix}
1\! & \!1\! & \!-1\! & \!1\! & \!1 \\ [-0.5ex] -3\! & \!-1\! &...
...
& \!-1\! & \!0 \\ [-0.5ex] 11\! & \!5\! & \!-5\! & \!a\! & \!a+2
\end{bmatrix}$](img1638.png) (21)
(21)
![$ \begin{bmatrix}
1\! & \!1\! & \!2\! & \!-3\! & \!4 \\ [-0.5ex] 0\! & \!2\! & \...
...4\! & \!-5\! & \!8
\\ [-0.5ex] 1\! & \!3\! & \!5\! & \!-7\! & \!9
\end{bmatrix}$](img1639.png)
(22)
![$ \begin{bmatrix}
1\! & \!3\! & \!1\! & \!-2\! & \!-3 \\ [-0.5ex] 1\! & \!4\! & ...
...! & \!-7\! & \!-3
\\ [-0.5ex] 3\! & \!8\! & \!1\! & \!-7\! & \!-8
\end{bmatrix}$](img1640.png) (23)
(23)
![$ \begin{bmatrix}
1\! & \!3\! & \!-2\! & \!5\! & \!4 \\ [-0.5ex] 1\! & \!4\! & \...
...2\! & \!4\! & \!3 \\ [-0.5ex]
2\! & \!7\! & \!-3\! & \!6\! & \!13
\end{bmatrix}$](img1641.png) (24)
(24)
![$ \begin{bmatrix}
1\! & \!2\! & \!-3\! & \!-2\! & \!-3 \\ [-0.5ex] 1\! & \!3\! &...
... & \!-2\! &
-11 \\ [-0.5ex] 2\! & \!1\! & \!-9\! & \!-10\! & \!-3
\end{bmatrix}$](img1642.png)
(25)
![$ \begin{bmatrix}
1\! & \!3\! & \!1\! & \!-3\! & \!2 \\ [-0.5ex] 1\! & \!3\! & \...
...\!-2\! & \!1\! & \!3 \\ [-0.5ex] 1\! &
2\! & \!2\! & \!-3\! & \!2
\end{bmatrix}$](img1643.png) (26)
(26)
![$ \begin{bmatrix}
1\! & \!4\! & \!-2\! & \!4\! & \!-5\! & \!4\! & \!1 \\ [-0.5ex...
...5 \\ [-0.5ex] 3\! &
10\! & \!-1\! & \!-9\! & \!6\! & \!8\! & \!-2
\end{bmatrix}$](img1644.png)
問 3.50 (連立 1 次方程式)
次の連立 1 次方程式の解を求めよ.
また,係数行列と拡大係数行列の階数を求めよ.
(1)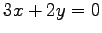 (2)
(2)
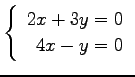 (3)
(3)
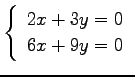 (4)
(4)
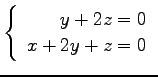
(5)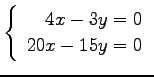 (6)
(6)
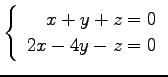 (7)
(7)
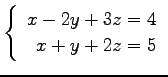
(8)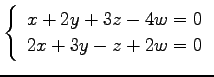 (9)
(9)
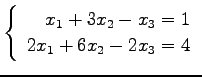 (10)
(10)
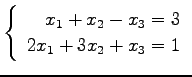
(11)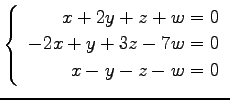 (12)
(12)
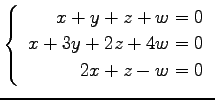 (13)
(13)
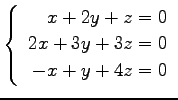
(14)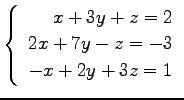 (15)
(15)
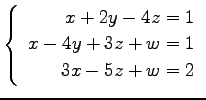 (16)
(16)
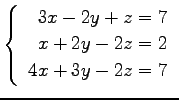
(17)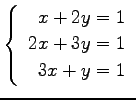 (18)
(18)
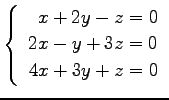 (19)
(19)
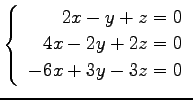
(20)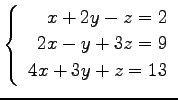 (21)
(21)
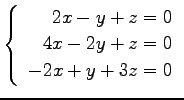 (22)
(22)
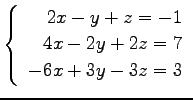
(23)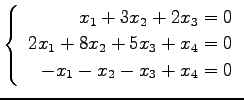 (24)
(24)
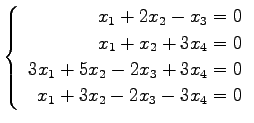
(25)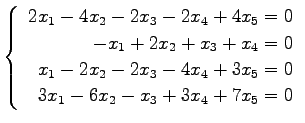 (26)
(26)
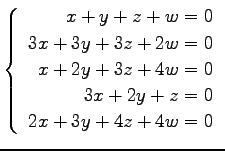
(27)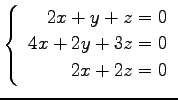 (28)
(28)
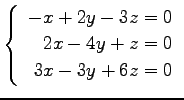 (29)
(29)
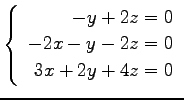
(30)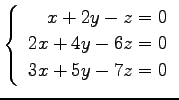 (31)
(31)
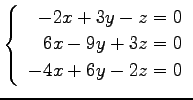 (32)
(32)
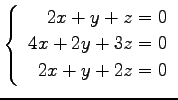
(33)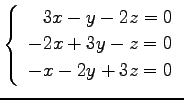 (34)
(34)
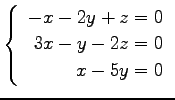 (35)
(35)
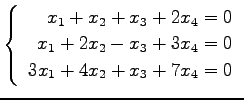
(36)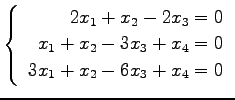 (37)
(37)
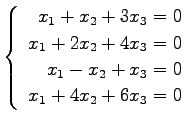 (38)
(38)
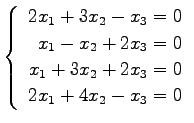
(39)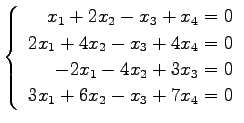 (40)
(40)
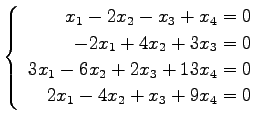
(41)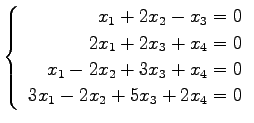 (42)
(42)
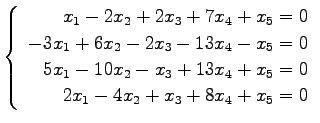
(43)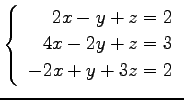 (44)
(44)
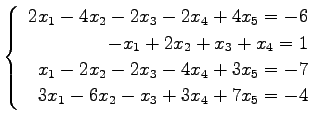
(45)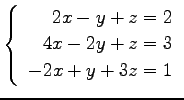 (46)
(46)
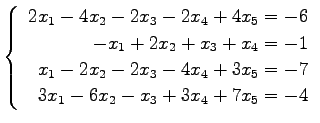
(47)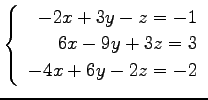 (48)
(48)
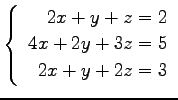 (49)
(49)
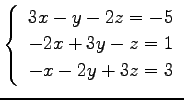
(50)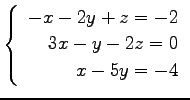 (51)
(51)
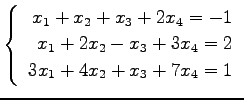 (52)
(52)
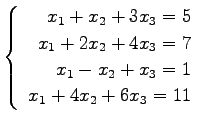
(53)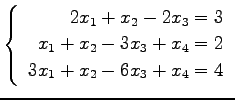 (54)
(54)
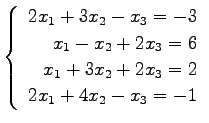
(55)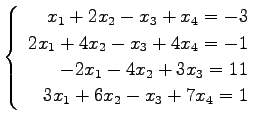 (56)
(56)
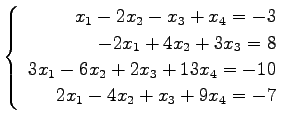
(57)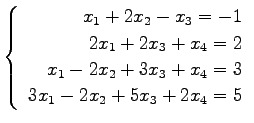 (58)
(58)
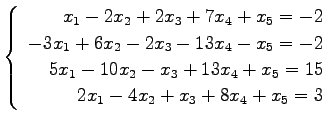
(1)
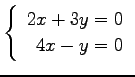 (3)
(3)
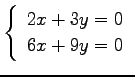 (4)
(4)
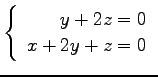
(5)
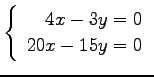 (6)
(6)
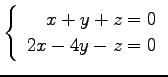 (7)
(7)
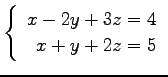
(8)
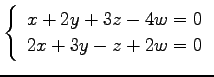 (9)
(9)
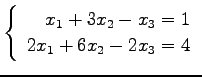 (10)
(10)
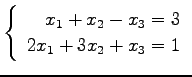
(11)
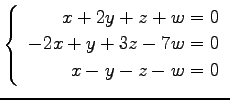 (12)
(12)
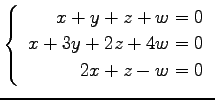 (13)
(13)
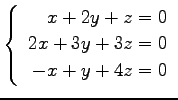
(14)
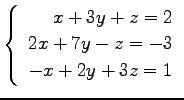 (15)
(15)
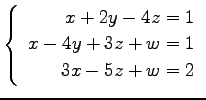 (16)
(16)
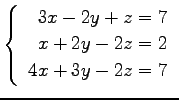
(17)
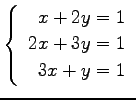 (18)
(18)
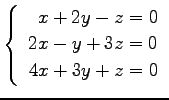 (19)
(19)
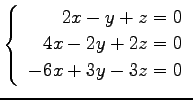
(20)
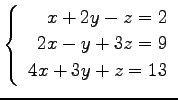 (21)
(21)
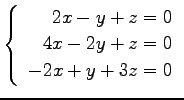 (22)
(22)
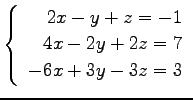
(23)
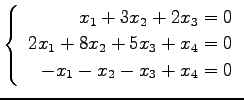 (24)
(24)
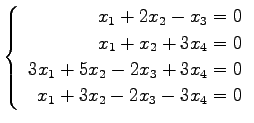
(25)
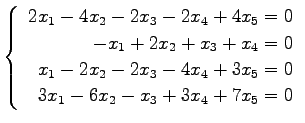 (26)
(26)
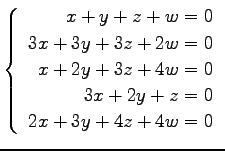
(27)
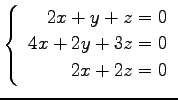 (28)
(28)
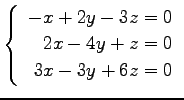 (29)
(29)
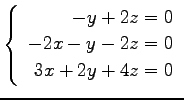
(30)
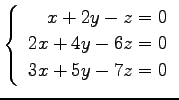 (31)
(31)
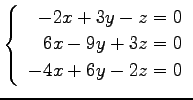 (32)
(32)
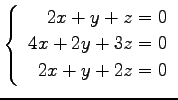
(33)
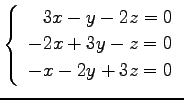 (34)
(34)
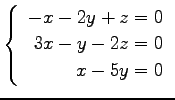 (35)
(35)
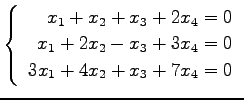
(36)
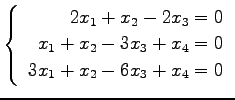 (37)
(37)
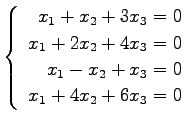 (38)
(38)
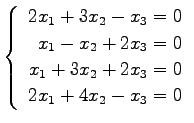
(39)
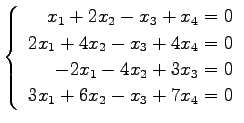 (40)
(40)
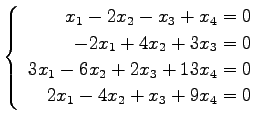
(41)
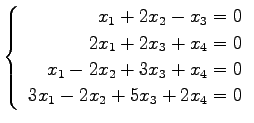 (42)
(42)
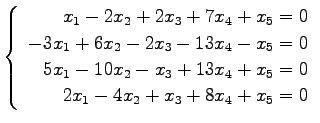
(43)
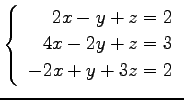 (44)
(44)
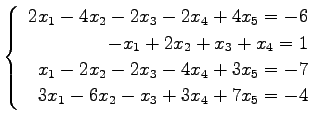
(45)
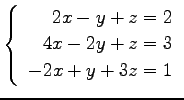 (46)
(46)
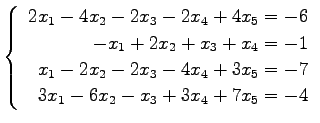
(47)
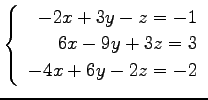 (48)
(48)
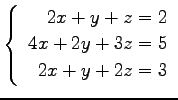 (49)
(49)
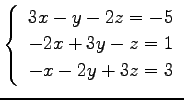
(50)
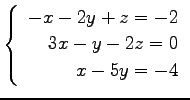 (51)
(51)
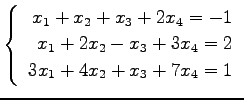 (52)
(52)
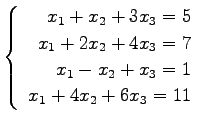
(53)
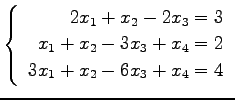 (54)
(54)
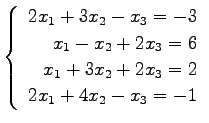
(55)
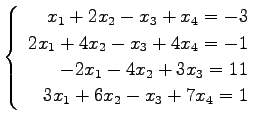 (56)
(56)
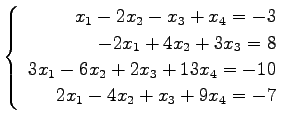
(57)
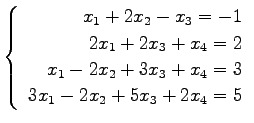 (58)
(58)
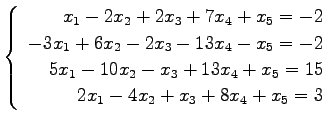
平成20年2月2日