3.12 ちょっとまとめ
? 3.45 (任意定数を含む解って何?)
方程式
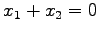 の解を考えよう.
この方程式の解はどのように表現したらよいだろうか.
まずは具体的にいくつか解を書き下してみよう.
解は方程式に代入して成り立てばよいから,
の解を考えよう.
この方程式の解はどのように表現したらよいだろうか.
まずは具体的にいくつか解を書き下してみよう.
解は方程式に代入して成り立てばよいから,
は解となるのがすぐ分かる. この解から予想できることとして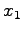 は任意の値で良さそうである.
これを
は任意の値で良さそうである.
これを 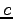 としよう.
としよう.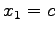 とおけば
とおけば 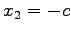 である.
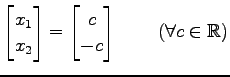
よって解として
である.
よって解として
を得る.確にこれが解となっているかは, 方程式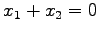 に代入すればよい.
この解は任意定数を含む解である.
変数の個数は
に代入すればよい.
この解は任意定数を含む解である.
変数の個数は 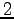 個であり,
方程式の本数が
個であり,
方程式の本数が 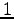 本であるので,
任意定数の個数は
本であるので,
任意定数の個数は 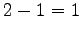 個となる.
個となる.
を考えよう.第一式は先ほどの方程式と同じである. であるから第一式を満たす解として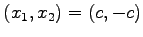 を得る.
第二式も第一式と同じ形をしており,
変数名が違うだけである.
よって解は
を得る.
第二式も第一式と同じ形をしており,
変数名が違うだけである.
よって解は
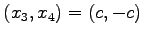 である.
しかし第一式と第二式とは独立しているので,
任意定数も独立してとり得る.
これを
である.
しかし第一式と第二式とは独立しているので,
任意定数も独立してとり得る.
これを
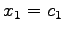 ,
,
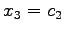 としよう.
よって解として
としよう.
よって解として
を得る. 変数が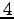 個,方程式が
個,方程式が 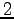 本,
任意定数が
本,
任意定数が 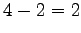 個である.
個である.
| (475) | ||
| (476) | ||
| (477) | ||
| (478) | ||
| (479) |
は解となるのがすぐ分かる. この解から予想できることとして
 |
(480) |
を得る.確にこれが解となっているかは, 方程式
次に方程式
![$\displaystyle \left\{\begin{array}{l} x_{1}+x_{2}=0 \\ [.5ex] x_{3}+x_{4}=0 \end{array}\right.$](img1590.png) |
(481) |
を考えよう.第一式は先ほどの方程式と同じである. であるから第一式を満たす解として
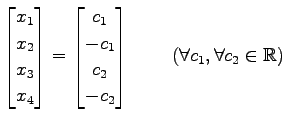 |
(482) |
を得る. 変数が
以上より, 任意定数の個数は変数の個数から方程式の(本質的な)本数を引い たものである.
? 3.46 (簡約化って何?)
方程式
を考えよう.第一式から第二式を引くと,
を得る. 第一式から変数が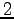 個減っている.
このとき係数行列は
個減っている.
このとき係数行列は
のように変形される. 右の行列は簡約な行列となっている.
を考えよう. 方程式と係数行列の変化をみよう:
このように基本変形により変数が減って行く. この手順によりうまく変数を減らすことができる. ある行列が与えられたとき, その行列に対して簡約な行列は一意に定まる. つまり,与えられた方程式に対して常に うまい変数の減らし方が存在することを意味する.
![$\displaystyle \left\{\begin{array}{ccccc} x_{1} & +x_{2} & +x_{3} & +x_{4} & =0 \\ [.5ex] & & x_{3} & +x_{4} & =0 \end{array}\right.$](img1597.png) |
(483) |
を考えよう.第一式から第二式を引くと,
![$\displaystyle \left\{\begin{array}{ccccc} x_{1} & +x_{2} & & & =0 \\ [.5ex] & & x_{3} & +x_{4} & =0 \end{array}\right.$](img1598.png) |
(484) |
を得る. 第一式から変数が
 |
(485) |
のように変形される. 右の行列は簡約な行列となっている.
次に方程式
![$\displaystyle \left\{\begin{array}{ccc} 3x_{1} & +\,4x_{2} & =2 \\ [.5ex] x_{1} & +\,2x_{2} & =3 \end{array}\right.$](img1600.png) |
(486) |
を考えよう. 方程式と係数行列の変化をみよう:
![$\displaystyle \left\{\begin{array}{ccc} 3x_{1} & +\,4x_{2} & =2 \\ [.5ex] x_{1}...
...\qquad \left[\begin{array}{cc\vert c} 3 & 4 & 2 \\ 1 & 2 & 3 \end{array}\right]$](img1601.png) |
(487) | |
![$\displaystyle \to \left\{\begin{array}{ccc} 0 & -\,2x_{2} & =-7 \\ [.5ex] x_{1}...
... \to \left[\begin{array}{cc\vert c} 0 & -2 & -7 \\ 1 & 2 & 3 \end{array}\right]$](img1602.png) |
(488) | |
![$\displaystyle \to \left\{\begin{array}{ccc} x_{1} & +\,2x_{2} & =3 \\ [.5ex] & ...
... \to \left[\begin{array}{cc\vert c} 1 & 2 & 3 \\ 0 & -2 & -7 \end{array}\right]$](img1603.png) |
(489) | |
![$\displaystyle \to \left\{\begin{array}{ccc} x_{1} & 0 & =-4 \\ [.5ex] & -2x_{2}...
...\to \left[\begin{array}{cc\vert c} 1 & 0 & -4 \\ 0 & -2 & -7 \end{array}\right]$](img1604.png) |
(490) | |
![$\displaystyle \to \left\{\begin{array}{ccc} x_{1} & & =-4 \\ [.5ex] & x_{2} & =...
...\to \left[\begin{array}{cc\vert c} 1 & 0 & -4 \\ 0 & 1 & 7/2 \end{array}\right]$](img1605.png) |
(491) |
このように基本変形により変数が減って行く. この手順によりうまく変数を減らすことができる. ある行列が与えられたとき, その行列に対して簡約な行列は一意に定まる. つまり,与えられた方程式に対して常に うまい変数の減らし方が存在することを意味する.
? 3.47 (ランクっ何?)
方程式
を考えよう. 変数が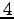 個,方程式が
個,方程式が 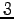 本であるから
任意定数は
本であるから
任意定数は 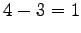 個であろう.
しかし本当にそうであろうか.
まずは方程式に基本変形をほどこしてみよう:
個であろう.
しかし本当にそうであろうか.
まずは方程式に基本変形をほどこしてみよう:
このように方程式は本質的に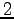 本である.
よって変数が
本である.
よって変数が 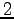 個,方程式が
個,方程式が 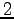 本,
任意定数が
本,
任意定数が 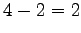 個となる.
これを係数行列でみてみよう:
個となる.
これを係数行列でみてみよう:
最後の簡約化された行列に着目する. 行列のランクは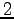 である.
つまり,係数行列のランクは
方程式の本質的な本数を示している.
である.
つまり,係数行列のランクは
方程式の本質的な本数を示している.
![$\displaystyle \left\{\begin{array}{ccccc} x_{1} & +\,x_{2} & +\,x_{3} & +\,x_{4...
... & =0 \\ [.5ex] 2x_{1} &+\,2x_{2} & +\,3x_{3}& +\,3x_{4}& =0 \end{array}\right.$](img1606.png) |
(492) |
を考えよう. 変数が
![$\displaystyle \left\{\begin{array}{ccccc} x_{1} & +x_{2} & & & =0 \\ [.5ex] & &...
...+x_{4} & =0 \\ [.5ex] 2x_{1} &+2x_{2} & +3x_{3}& +3x_{4}& =0 \end{array}\right.$](img1608.png) |
(493) | |
![$\displaystyle \left\{\begin{array}{ccccc} x_{1} & +x_{2} & & & =0 \\ [.5ex] & & x_{3} & +x_{4} & =0 \\ [.5ex] 0 & +0 & +0 & +0 & =0 \end{array}\right.$](img1609.png) |
(494) | |
![$\displaystyle \left\{\begin{array}{ccccc} x_{1} & +x_{2} & & & =0 \\ [.5ex] & & x_{3} & +x_{4} & =0 \end{array}\right.$](img1598.png) |
(495) |
このように方程式は本質的に
 |
(496) |
最後の簡約化された行列に着目する. 行列のランクは
まとめ 3.48 (連立 1 次方程式についてのまとめ)
連立 1 次方程式
について次の関係が成り立つ:
(II) 同次形(
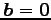 )のとき
)のとき
| (497) |
について次の関係が成り立つ:
(I) 非同次形(
![]() )のとき
)のとき
|
|
|
解なし |
|
|
|
一意な解をもつ |
|
|
|
任意定数を含む解をもつ |
|
任意定数の個数 |
| 常に |
|
が成り立つので | 解を常にもつ |
|
|
|
自明な解(
|
|
|
|
|
|
任意定数を含む解をもつ |
|
任意定数の個数 |
平成20年2月2日