1.35 点と平面との距離
定義 1.168 (点と平面との距離)
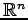 空間内の点
空間内の点  と平面を考える.
点
と平面を考える.
点  と平面上の点
と平面上の点  との距離が最小となるとき,
その距離を点と平面との距離という.
との距離が最小となるとき,
その距離を点と平面との距離という.
定理 1.169 (点と平面との距離)
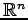 空間内の点
空間内の点  と平面を考える.
点
と平面を考える.
点  と平面上の点
と平面上の点  との距離が最小となるのは
直線
との距離が最小となるのは
直線 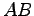 と平面が直交するときである.
と平面が直交するときである.
例 1.170 (点と平面との距離)
点 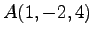 の平面
の平面
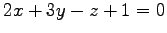 への
正射影は
への
正射影は
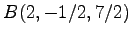 である.
直線
である.
直線 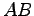 は平面に直交する.
距離
は平面に直交する.
距離
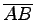 が点と平面との距離である.
よって距離は
が点と平面との距離である.
よって距離は
である.
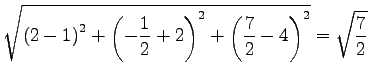 |
(233) |
である.
定理 1.171 (点と平面との距離)
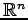 空間内の点
空間内の点
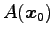 と
超平面
と
超平面
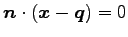 を考える.
点
を考える.
点  と平面との距離は
と平面との距離は
である.
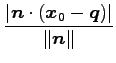 |
(234) |
である.
問 1.172 (点と平面との距離)
これを示せ.
であるから,
より,
を得る.
(証明)
点
![]() から平面
から平面
![]() への
正射影を
への
正射影を
![]() とする.
距離
とする.
距離
![]() が
点と平面の距離である.
正射影
が
点と平面の距離である.
正射影
![]() は
は
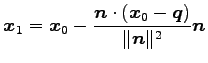 |
(235) |
であるから,
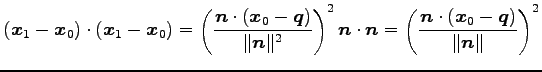 |
(236) |
より,
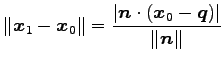 |
(237) |
を得る.
平成20年2月2日