1.25 点と直線との距離
定義 1.130 (点と直線との距離)
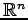 空間内の点
空間内の点  と直線
と直線 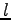 を考える.
点
を考える.
点  と
と 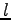 上の点
上の点  との距離が最小となるとき,
その距離を点と直線との距離という.
との距離が最小となるとき,
その距離を点と直線との距離という.
定理 1.131 (点と直線との距離)
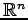 空間内の
点
空間内の
点  と直線
と直線 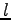 を考える.
点
を考える.
点  と
と 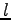 上の点
上の点  との距離が最小となるのは,
直線
との距離が最小となるのは,
直線 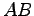 と直線
と直線 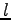 が直交するときである.
が直交するときである.
問 1.132 (点と直線との距離)
これを示せ.
より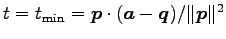 のとき
最小値
のとき
最小値
をとる. このとき
が成り立つ.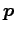 と
と
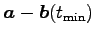 とは直交する.
とは直交する.
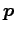 は直線
は直線 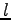 の方向ベクトルであり,
の方向ベクトルであり,
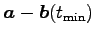 は直線
は直線 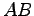 の方向ベクトルである.
よって距離が最小になるとき直線
の方向ベクトルである.
よって距離が最小になるとき直線 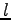 と直線
と直線 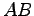 は直交する.
は直交する.
(証明)
点
![]() ,
,
![]() とする.
点
とする.
点 ![]() を直線
を直線 ![]() 上の点とする.
すなわち
上の点とする.
すなわち
![]() とおく.
点
とおく.
点 ![]() と
と ![]() の距離を考える.
の距離を考える.
| (143) | ||
| (144) | ||
| (145) | ||
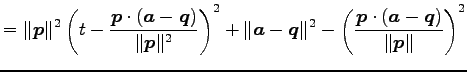 |
(146) |
より
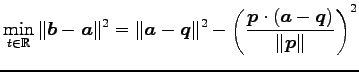 |
(147) |
をとる. このとき
| (148) | ||
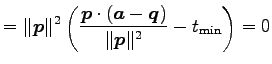 |
(149) |
が成り立つ.
例 1.133 (点と直線の距離)
点 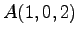 ,
, 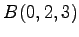 ,
,
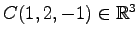 において,
点
において,
点 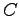 と直線
と直線 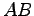 を考える.
点
を考える.
点 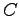 から直線
から直線 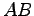 への正射影は
への正射影は
であるら,距離は
より求まる.
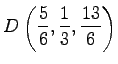 |
であるら,距離は
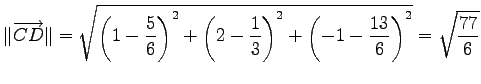 |
より求まる.
定理 1.134 (点と直線の距離)
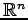 空間内の
点
空間内の
点
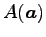 と直線
と直線
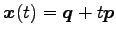 との距離は
との距離は
である.
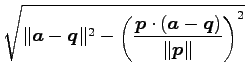 |
(150) |
である.
問 1.135 (点と直線の距離)
これを示せ.
である. ここで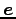 は直線の単位方向ベクトルであり
は直線の単位方向ベクトルであり
 となることに注意する.
点
となることに注意する.
点  ,
,  との距離は
との距離は
より得られる.
(証明その1)
問 ![[*]](crossref.png) の証明より
の証明より
![]() のとき
点と直線の距離であるから,
(
のとき
点と直線の距離であるから,
(![[*]](crossref.png) )より明らか.
)より明らか.
(証明その2)
点
![]() の直線
の直線
![]() への正射影
への正射影
![]() を考える.
このとき
を考える.
このとき
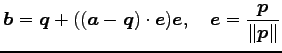 |
(151) |
である. ここで
| (152) | ||
| (153) | ||
| (154) | ||
| (155) | ||
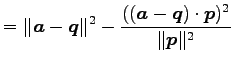 |
(156) |
より得られる.
例 1.136 (
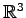 内の点と直線の距離)
点
内の点と直線の距離)
点 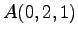 と直線
と直線
![$ \vec{x}(t)=\begin{bmatrix}{1}\\ [-.5ex]{3}\\ [-.5ex]{-1}\end{bmatrix}+t\begin{bmatrix}{2}\\ [-.5ex]{-1}\\ [-.5ex]{1}\end{bmatrix}$](img678.png) との
距離を考える.
との
距離を考える.
であるから,距離は
である.
![$ \vec{x}(t)=\begin{bmatrix}{1}\\ [-.5ex]{3}\\ [-.5ex]{-1}\end{bmatrix}+t\begin{bmatrix}{2}\\ [-.5ex]{-1}\\ [-.5ex]{1}\end{bmatrix}$](img678.png) との
距離を考える.
との
距離を考える.
| (157) |
であるから,距離は
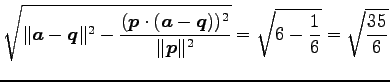 |
(158) |
である.
例 1.137 (
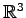 内の点と直線の距離)
点
内の点と直線の距離)
点 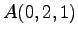 と直線
と直線
![$ \vec{x}(t)=\begin{bmatrix}{1}\\ [-.5ex]{3}\\ [-.5ex]{-1}\end{bmatrix}+t\begin{bmatrix}{2}\\ [-.5ex]{-1}\\ [-.5ex]{1}\end{bmatrix}$](img678.png) との
距離を考える.
点
との
距離を考える.
点  から直線への正射影を
から直線への正射影を
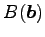 とする.
とする.
であるから,
より,
である.点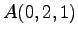 と点
と点
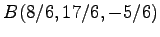 との距離が
点
との距離が
点  と直線の距離であるから,
と直線の距離であるから,
より
である.
![$ \vec{x}(t)=\begin{bmatrix}{1}\\ [-.5ex]{3}\\ [-.5ex]{-1}\end{bmatrix}+t\begin{bmatrix}{2}\\ [-.5ex]{-1}\\ [-.5ex]{1}\end{bmatrix}$](img678.png) との
距離を考える.
点
との
距離を考える.
点 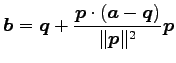 |
(159) |
であるから,
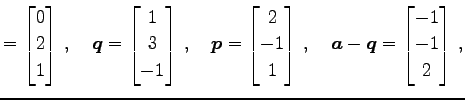 |
(160) | |
| (161) |
より,
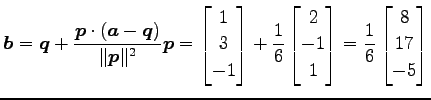 |
(162) |
である.点
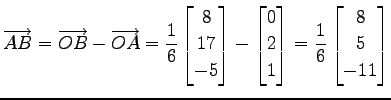 |
(163) |
より
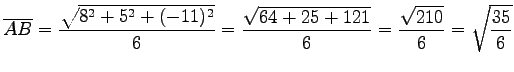 |
(164) |
である.
平成20年2月2日