4.19 行列式と面積
行列式の図形上の意味を考える.
まず ![]() のときを考える.
のときを考える.
![$\displaystyle S=\pm \begin{vmatrix}a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}= \pm \det \bigl[\vec{a}_{1}\,\,\vec{a}_{2}\bigr]$](img2327.png) |
(800) |
は頂点が
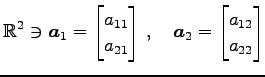 |
(801) |
である. 符号は
![$\displaystyle V=\pm \begin{vmatrix}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} ...
...}\,\,\vec{a}_{2}\,\,\vec{a}_{3}\bigr]= \pm[\vec{a}_{1},\vec{a}_{2},\vec{a}_{3}]$](img2334.png) |
(802) |
は頂点が
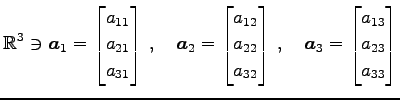 |
(803) |
である.
平成20年2月2日
4.19 行列式と面積
行列式の図形上の意味を考える. まず
のときを考える.
(800)
は頂点が,
,
,
である平行四辺形の面積となる. ただし
(801)
である. 符号はから
が反時計回りのときが正であり, 時計回りのとき負である.
(802)
は頂点が,
,
,
,
,
,
,
である平行 6 面体の体積となる. ただし
(803)
である.は スカラー三重積であることに注意する. 符号は
,
,
が 右手系のとき正であり, 左手系のとき負となる.
平成20年2月2日