6.18 三角関数の定積分
問 6.84 (三角関数の定積分)
自然数 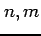 に対して
に対して
となることを示せ(ヒント:積和の公式). ただし,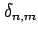 はクロネッカーのデルタ(Kronecker's
delta) である.
はクロネッカーのデルタ(Kronecker's
delta) である.
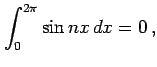 |
||
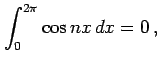 |
||
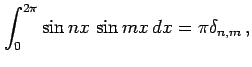 |
||
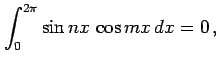 |
||
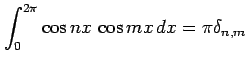 |
となることを示せ(ヒント:積和の公式). ただし,
平成19年10月3日
6.18 三角関数の定積分
問 6.84 (三角関数の定積分) 自然数に対して
となることを示せ(ヒント:積和の公式). ただし,はクロネッカーのデルタ(Kronecker's delta) である.
平成19年10月3日