6.5 部分積分法
定理 6.18 (部分積分法)
これを部分積分法(integration by parts)という.
を得る.これを両辺を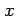 で積分すると
で積分すると
となる.移項すると証明終了.
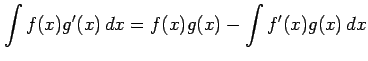 |
これを部分積分法(integration by parts)という.
(証明)
関数 ![]() を微分すると積の微分公式より
を微分すると積の微分公式より
を得る.これを両辺を
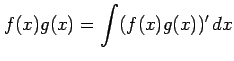 |
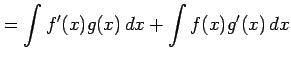 |
となる.移項すると証明終了.
例 6.19 (部分積分法の使用例)
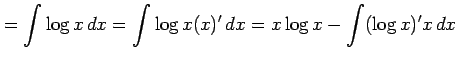 |
||
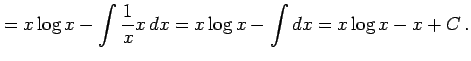 |
例 6.20 (部分積分法の使用例)
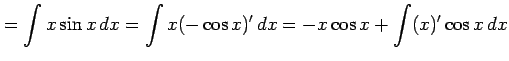 |
||
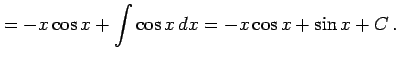 |
例 6.21 (部分積分法の使用例)
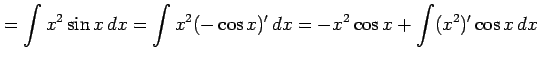 |
||
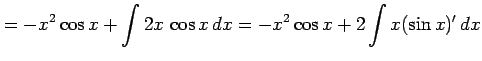 |
||
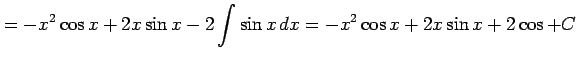 |
||
例 6.22 (部分積分法の使用例)
より,
であり,
を得る.
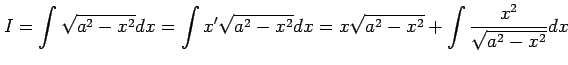 |
||
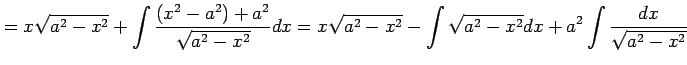 |
||
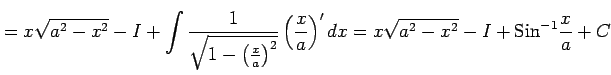 |
より,
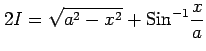 |
であり,
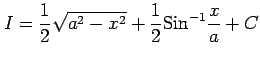 |
を得る.
例 6.23 (部分積分法の使用例)
不定積分
を求める.部分積分より
が成り立つ.これは
と書ける.よって,
を得る.
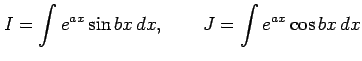 |
を求める.部分積分より
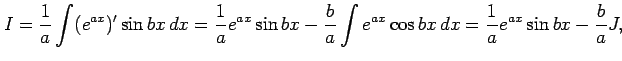 |
||
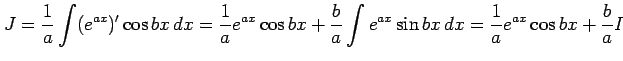 |
が成り立つ.これは
と書ける.よって,
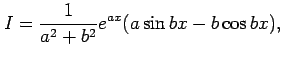 |
||
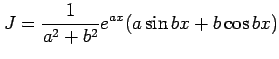 |
を得る.
例 6.24 (漸化式による不定積分の求積)
不定積分
を考える.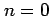 のとき
のとき
を得る.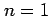 のとき
のとき
を得る.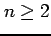 のときを考える.
のときを考える.
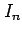 を部分積分を用いて計算すると
を部分積分を用いて計算すると
となる.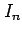 を移項すると
を移項すると
を得る. 最後の式は漸化式である. この漸化式より不定積分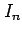 が求まる.
同様にして
が求まる.
同様にして
を得る.
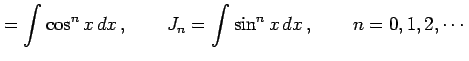 |
を考える.
 |
を得る.
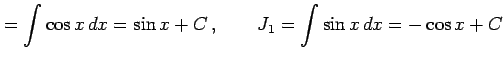 |
を得る.
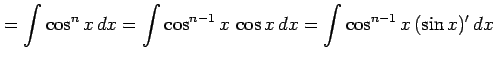 |
||
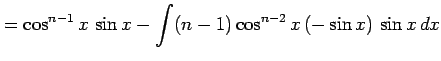 |
||
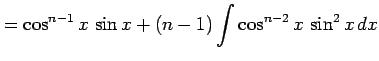 |
||
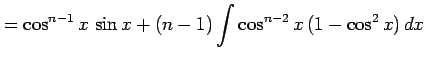 |
||
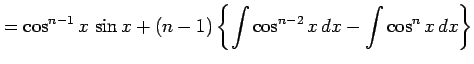 |
||
となる.
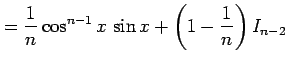 |
を得る. 最後の式は漸化式である. この漸化式より不定積分
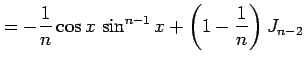 |
を得る.
問 6.25 (漸化式による不定積分の求積)
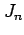 についての漸化式を求めよ.
についての漸化式を求めよ.
注意 6.26 (三角関数の不定積分の計算例)
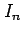 ,
, 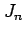 は
は 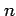 倍角の公式を用いても求積される.
倍角の公式を用いても求積される.
平成19年10月3日