4.5 線形変換
定義 4.23 (線形変換)
ベクトル空間 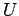 から自分自身への線形写像
から自分自身への線形写像 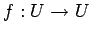 を
線形変換(linear transformation)という.
を
線形変換(linear transformation)という.
定理 4.24 (線形写像の表現行列)
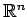 の基底を
の基底を
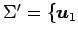 ,
,  ,
,
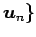 とし,
座標を
とし,
座標を 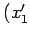 ,
,  ,
,
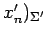 とおく.
このとき,
任意の線形変換
とおく.
このとき,
任意の線形変換
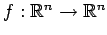 は
は
と行列表示で書ける. ただし, は
は
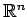 の標準基底
の標準基底 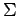 に関する
に関する  の表現行列とする.
また,
の表現行列とする.
また, 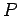 は
は 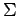 に対する
に対する 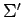 の基底の変換行列であり,
の基底の変換行列であり,
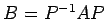 を
を
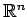 の基底
の基底 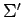 に関する表現行列という.
に関する表現行列という.
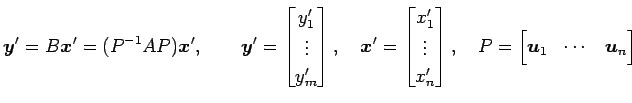 |
と行列表示で書ける. ただし,
例 4.25 (線形変換の表現行列の基底の取り替えの具体例)
線形変換
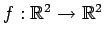 ;
;
の基底
における表現行列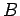 を求める.
を求める.
 の任意のベクトルは
の任意のベクトルは
と表される.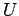 は
は
 の
標準基底
の
標準基底
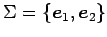 に対する
基底
に対する
基底
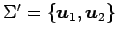 の基底の変換行列であり,
の基底の変換行列であり,
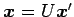 は
座標
は
座標
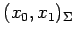 から
座標
から
座標
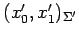 への座標変換を表す.
への座標変換を表す.
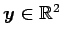 であるから,
同様に
であるから,
同様に
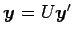 が成り立つ.
これより,
が成り立つ.
これより,
となるので,
が成立する. よって基底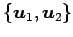 に関する
に関する
 の表現行列
の表現行列 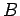 は
は
により定まる. また,基底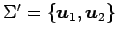 に関する
行列表示は
に関する
行列表示は
であり,
とも書ける. 座標系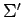 において線形写像
において線形写像  は,
は,
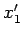 軸方向は変化せず,
軸方向は変化せず,
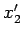 軸方向は
軸方向は 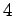 倍となる変換である.
倍となる変換である.
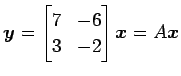 |
の基底
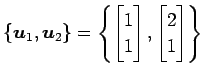 |
における表現行列
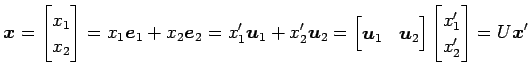 |
と表される.
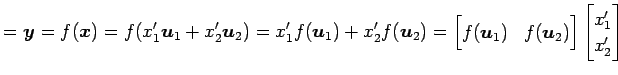 |
||
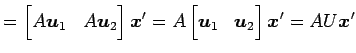 |
となるので,
が成立する. よって基底
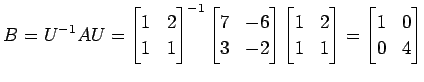 |
により定まる. また,基底
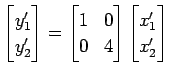 |
であり,
とも書ける. 座標系
Kondo Koichi

平成18年1月17日