4.6 一般の線形写像の表現行列
![]() 次元のベクトル空間
次元のベクトル空間 ![]() と
と
![]() 次元のベクトル空間
次元のベクトル空間 ![]() において,
基底をそれぞれ
において,
基底をそれぞれ
![]() ,
,
![]() とすると,
とすると,
![]() ,
, ![]() の任意のベクトルはそれぞれ
の任意のベクトルはそれぞれ
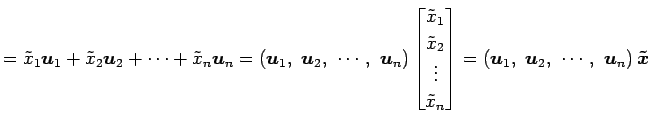 |
||
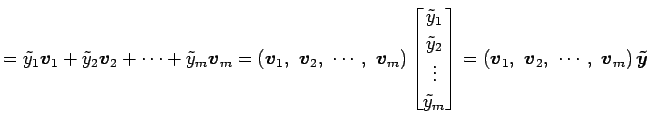 |
と表される. このとき, 線形写像
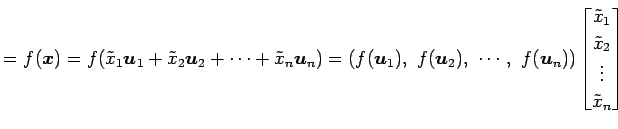 |
||
となる. ベクトル
と表されるので
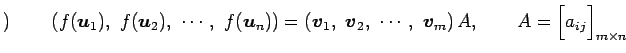 |
と書ける. 以上より(▲), (☆), (★)より
を得る.
が成り立つ. 線形写像
注意 4.26 (一般のベクトル空間における線形写像)
一般のベクトル空間における線形写像 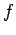 と
数ベクトル空間における線形写像
と
数ベクトル空間における線形写像 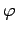 とを
次のように同一視する:
とを
次のように同一視する:
定義 4.27 (線形写像の表現行列)
ベクトル空間 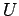 の基底を
の基底を
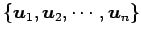 とし,
ベクトル空間
とし,
ベクトル空間 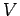 の基底を
の基底を
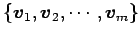 とする.
このとき,
線形写像
とする.
このとき,
線形写像 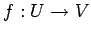 が
が
をみたすとき, 行列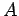 を
を 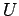 の基底
の基底
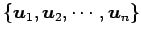 と
と
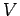 の基底
の基底
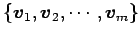 に関する
表現行列という.
に関する
表現行列という.
をみたすとき, 行列
定理 4.28 (線形写像の行列表示)
線形写像 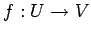 において,
ベクトル空間
において,
ベクトル空間 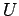 の基底が
の基底が
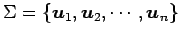 であり,
その基底における座標を
であり,
その基底における座標を
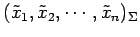 とし,
ベクトル空間
とし,
ベクトル空間 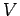 の基底が
の基底が
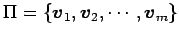 であり,
その基底における座標を
であり,
その基底における座標を
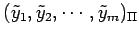 とする.
このとき,
行列
とする.
このとき,
行列 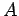 が
が 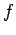 の表現行列であることと,
の表現行列であることと,
が成り立つこととは,必要十分条件である.
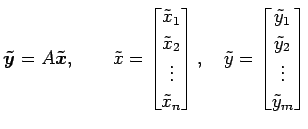 |
が成り立つこととは,必要十分条件である.
注意 4.29 (表現行列)
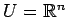 ,
,
 とし,
とし,
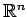 の基底を標準基底
の基底を標準基底
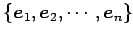 とし,
とし,
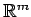 の基底を標準基底
の基底を標準基底
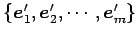 とする.
このとき
とする.
このとき
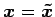 ,
,
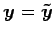 となるから,
(♭)は
となるから,
(♭)は
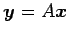 となる.
よって,
本節の表現行列の定義により定まる
となる.
よって,
本節の表現行列の定義により定まる 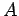 と
前節の表現行列の定義により定まる
と
前節の表現行列の定義により定まる 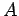 とは,
この条件のもとで一致する.
とは,
この条件のもとで一致する.
注意 4.30 (表現行列)
線形写像
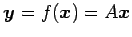 の標準基底に
おける表現行列は
の標準基底に
おける表現行列は 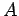 である.
である.
定理 4.31 (基底を取り換えたときの表現行列)
線形写像 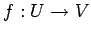 において
において
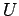 の基底
の基底
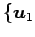 ,
,
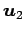 ,
, 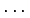 ,
,
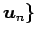 と
と
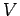 の基底
の基底
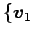 ,
,
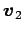 ,
, 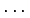 ,
,
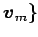 に
関する表現行列を
に
関する表現行列を  とする.
すなわち,
とする.
すなわち,
とする. の基底
の基底
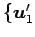 ,
,
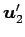 ,
, 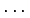 ,
,
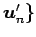 と
と
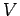 の基底
の基底
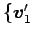 ,
,
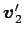 ,
, 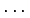 ,
,
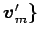 に
関する表現行列を
に
関する表現行列を 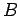 とする.
すなわち,
とする.
すなわち,
とする. このとき
が成り立つ. ここで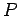 ,
, 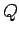 は基底の変換行列であり,
は基底の変換行列であり,
である.
が成り立つ.また,
となる.よって,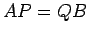 であり
であり
が成り立つ.
とする.
とする. このとき
が成り立つ. ここで
である.
(証明) まず,
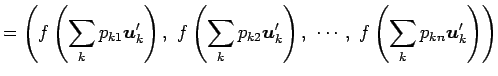 |
||
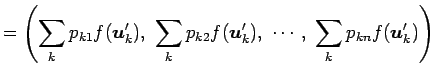 |
||
が成り立つ.また,
となる.よって,
が成り立つ.
定理 4.32 (線形変換の表現行列の基底の取り替え)
ベクトル空間  の基底
の基底
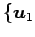 ,
,  ,
,
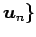 における
線形変換
における
線形変換 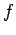 の表現行列を
の表現行列を 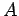 とし,
基底
とし,
基底
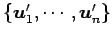 における
における
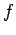 の表現行列を
の表現行列を 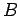 とする.
また,基底
とする.
また,基底
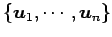 から
基底
から
基底
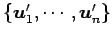 への
基底の変換行列を
への
基底の変換行列を 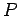 とする.
このとき
とする.
このとき
が成り立つ.
をみたす.基底の変換行列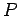 は
は
をみたす. このとき
が成り立つので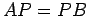 となる.
よって
となる.
よって
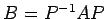 を得る.
を得る.
が成り立つ.
(証明)
まず,表現行列 ![]() ,
, ![]() は定義より
は定義より
をみたす.基底の変換行列
をみたす. このとき
が成り立つので
例 4.33 (表現行列の基底の取り替えの具体例)
線形変換
![$ F:\mathbb{R}[x]_2\to\mathbb{R}[x]_2$](img1998.png) ;
;
の表現行列を求める.![$ \mathbb{R}[x]_2$](img410.png) の基底を
の基底を
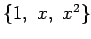 とし,
多項式
とし,
多項式 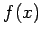 ,
, 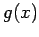 を表すと
を表すと
となる. このとき(☆)より
となる. ここで,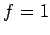 ,
, 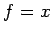 ,
, 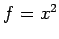 を(☆)に代入すると
それぞれ
を(☆)に代入すると
それぞれ 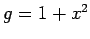 ,
, 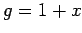 ,
, 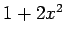 となるので,
となるので,
を得る. は基底
は基底
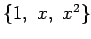 に関する
に関する 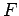 の表現行列である.
これを代入すると
の表現行列である.
これを代入すると
となる. (▲)と比較すると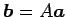 が成立する.
よって,線形変換
が成立する.
よって,線形変換 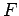 は
は
と行列表示で書かれた線形変換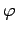 と等価である.
と等価である.
をみたす. 基底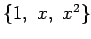 から
から
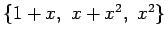 への
変換行列
への
変換行列 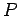 は
は
により与えられる. このとき,多項式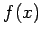 ,
, 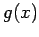 は
は
となる. (△), (▲)と(□), (■)とを比較すると
を得る. これは基底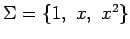 における
座標
における
座標
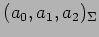 と
基底
と
基底
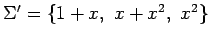 における
座標
における
座標
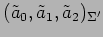 との座標変換を表す.
(♭), (□), (■)より
との座標変換を表す.
(♭), (□), (■)より
となるので,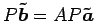 となり,
となり,
を得る. 以上より基底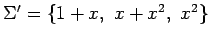 に関する
に関する
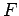 の表現行列
の表現行列 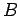 は
は
と得られる. よって,基底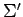 に関する線形変換
に関する線形変換 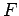 の行列表示は
の行列表示は
となる.
の表現行列を求める.
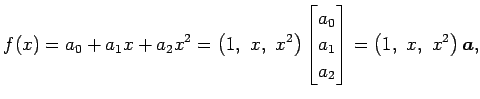 |
||
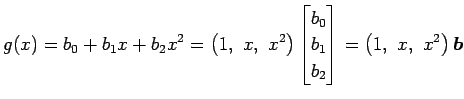 |
となる. このとき(☆)より
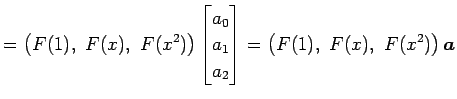 |
となる. ここで,
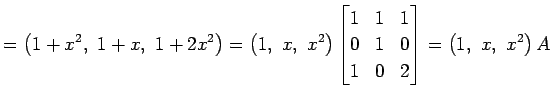 |
を得る.
となる. (▲)と比較すると
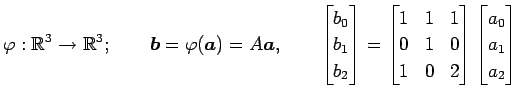 |
と行列表示で書かれた線形変換
次に基底
![]() に関する
表現行列
に関する
表現行列 ![]() を求める.
すなわち,
を求める.
すなわち,![]() は
は
をみたす. 基底
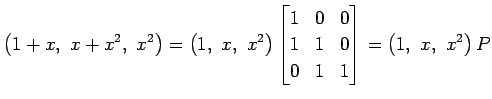 |
により与えられる. このとき,多項式
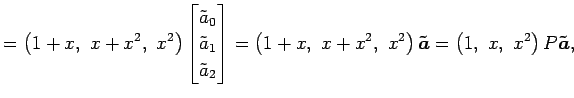 |
||
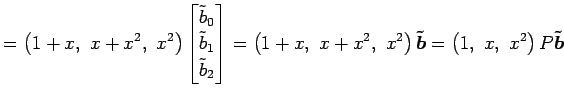 |
となる. (△), (▲)と(□), (■)とを比較すると
を得る. これは基底
となるので,
を得る. 以上より基底
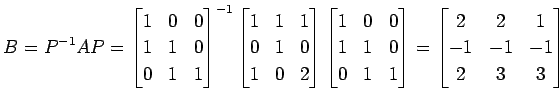 |
と得られる. よって,基底
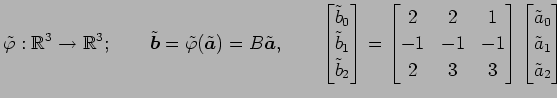 |
となる.
Kondo Koichi

平成18年1月17日