5.13 相似変換
定理 5.33 (相似変換)
行列  と行列
と行列
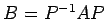 との固有値は等しい.
ただし
との固有値は等しい.
ただし 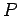 はある正則行列とする.
はある正則行列とする.
となるので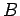 と
と  の固有値は等しい.
の固有値は等しい.
(証明)
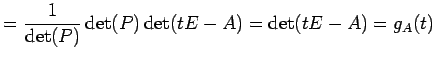 |
となるので
定義 5.34 (相似)
正方行列  ,
, 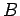 に対して
に対して
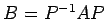 をみたすある正則行列
をみたすある正則行列 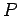 が存在するとき,
が存在するとき,
 と
と 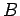 とは相似(similar)または
同値(equivalent)であるという.
とは相似(similar)または
同値(equivalent)であるという.
定義 5.35 (相似変換)
正方行列  がある正則行列
がある正則行列 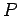 を用いて,
正方行列
を用いて,
正方行列
へ変換されるとき, この変換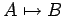 を
相似変換(similarity transformation)または
同値変換(equivalent transformation)という.
を
相似変換(similarity transformation)または
同値変換(equivalent transformation)という.
へ変換されるとき, この変換
Kondo Koichi

平成18年1月17日