5.12 演習問題 〜 固有値
問 5.31 (固有値)
次の行列の固有値とその固有値に属する固有ベクトルを求めよ.
(1)
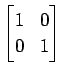 (2)
(2)
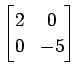 (3)
(3)
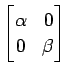 (4)
(4)
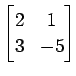 (5)
(5)
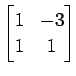
(6)
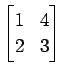 (7)
(7)
 (8)
(8)
 (9)
(9)
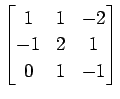
(10)
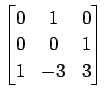 (11)
(11)
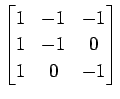 (12)
(12)
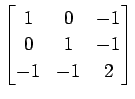 (13)
(13)

問 5.32 (固有空間)
次の線形変換の固有値とその固有空間を求めよ.
また,固有ベクトルを基底として選べるとき,
この基底に関する線形変換の表現行列を求めよ.
さらには,ベクトル空間が固有空間で直和分解されることを示せ.
(1)
![]() ; 点
; 点 ![]() と原点
と原点 ![]() と
と
![]() との中点
との中点 ![]() への変換
への変換
![]() .
(2)
.
(2)
![]() ; 点
; 点 ![]() から
原点
から
原点 ![]() を通り方向ベクトルが
を通り方向ベクトルが
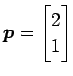 の直線への正射影
と
の直線への正射影
と ![]() との中点
との中点 ![]() への変換
への変換
![]() .
.
(3)
![]() ; 点
; 点 ![]() から平面
から平面
![]() への正射影
への正射影
![]() への射影変換
への射影変換
![]() .
.
(4)
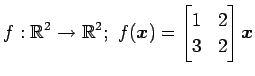 (5)
(5)
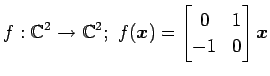
(6)
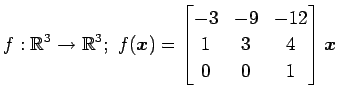 (7)
(7)
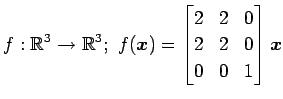
(8)
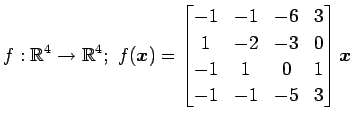 (9)
(9)
![$ \displaystyle{
F:\mathbb{R}[x]_{2}\to\mathbb{R}[x]_{2};\,\,
F(f)(x)=\int_0^{x}f(y)\,dy
}$](img2919.png)
(10)
![]() (11)
(11)
![]()
(12)
![]() (13)
(13)
![]()
(14)
![]()
(15)
![]()
(16)
![]()
Kondo Koichi

平成18年1月17日