5.9 固有多項式とトレース
定義 5.23 (トレース)
行列
![$ A=[a_{ij}]_{n\times n}$](img2841.png) に対して
に対して
を のトレース(trace)という.
のトレース(trace)という.
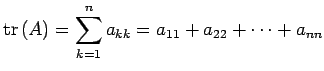 |
を
定理 5.24 (固有多項式とトレース)
行列
![$ A=[a_{ij}]_{n\times n}$](img2841.png) の
固有値が
の
固有値が
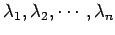 であるとする.
このとき,
であるとする.
このとき,
が成り立つ.
が成り立つ. 一方,
が成り立つ.ここで,
とおいた. 以上より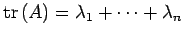 ,
,
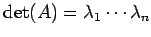 を得る.
を得る.
が成り立つ.
(証明)
固有値は ![]() ,
, ![]() ,
, ![]() であるから,
であるから,
が成り立つ. 一方,
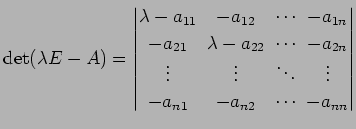 |
||
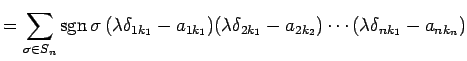 |
||
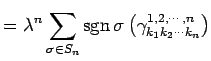 |
||
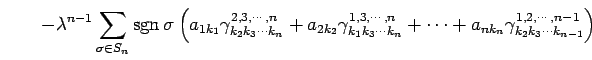 |
||
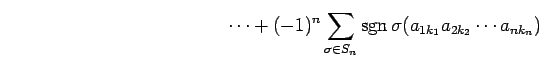 |
||
が成り立つ.ここで,
とおいた. 以上より
注意 5.25 (固有多項式)
 の固有多項式は
の固有多項式は
と表される.
と表される.
Kondo Koichi

平成18年1月17日