5.10 ケイリー・ハミルトンの定理
定義 5.26 (行列の多項式)
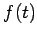 を多項式
を多項式
とする. このとき正方行列 に対して
に対して 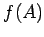 を
を
と定義する.
とする. このとき正方行列
と定義する.
定理 5.27 (ケイリー・ハミルトンの定理)
正方行列  の固有多項式を
の固有多項式を 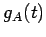 とする.
このとき
とする.
このとき
が成り立つ. これをケイリー・ハミルトン(Caley-Hamilton)の定理 という.
が成り立つ. これをケイリー・ハミルトン(Caley-Hamilton)の定理 という.
例 5.28 (ケイリー・ハミルトンの定理の使用例)
正方行列
の固有多項式は
である. このとき ケイリー・ハミルトンの定理より
が成り立つ. これを用いて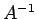 ,
, 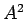 ,
, 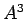 ,
, 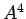 を求める.
(☆)の両辺に
を求める.
(☆)の両辺に 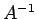 を左から掛けると
を左から掛けると
となる. これを変形して
を得る. 次に(☆)を変形して
を得る. さらに(♭)を用いて
を得る.
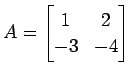 |
の固有多項式は
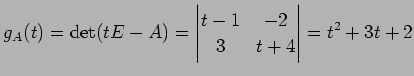 |
である. このとき ケイリー・ハミルトンの定理より
が成り立つ. これを用いて
となる. これを変形して
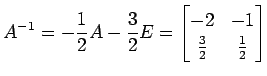 |
を得る. 次に(☆)を変形して
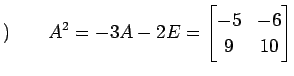 |
を得る. さらに(♭)を用いて
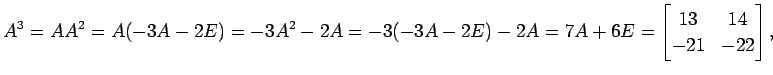 |
||
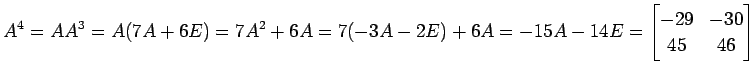 |
を得る.
問 5.29 (ケイリー・ハミルトンの定理の使用例)
この例題において 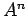 を求めよ.
を求めよ.
とおく.このとき
となる.よって漸化式
を得る. これは漸化式
とも表される.この一般項は
となる. よって
を得る.
(答え) まず
とおく.このとき
となる.よって漸化式
を得る. これは漸化式
とも表される.この一般項は
となる. よって
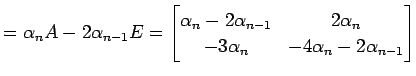 |
||
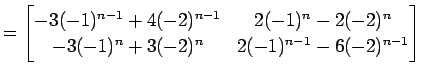 |
を得る.
Kondo Koichi

平成18年1月17日