5.8
![$ \mathbb{R}[x]_2$](img410.png) �ˤ����������Ѵ��θ�ͭ����
�ˤ����������Ѵ��θ�ͭ����
�� 5.20 (¿�༰�ζ��֤ˤ������ͭ������ζ�����)
�����Ѵ�
![$ F:\mathbb{R}[x]_2\to\mathbb{R}[x]_2$](img1998.png) ;
;
�θ�ͭ�͡���ͭ���֤���롥
�Ƚ롥 ���ΤȤ��� ��
�� 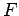 �Ǽ̤���
�Ǽ̤���
�Ȥʤ롥 ������
�Ǥ��뤫�顤���������
�������롥 ��
�� 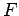 ���
�δ��� 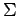 �˴ؤ���ɽ������Ǥ��롥
�ޤ������η�̤�
�˴ؤ���ɽ������Ǥ��롥
�ޤ������η�̤�
�Ȥ��Ƥ������롥 (��)��(��)��ꡤ �����Ѵ�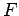 ��
��
�ˤ���������������Ѵ�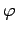 �������Ǥ��롥
�������Ǥ��롥
��ɽ�����Τǡ� ��ͭ��������
�������Ǥ��롥 �Ĥޤ���� �˴ؤ����ͭ�������Ф褤��
�˴ؤ����ͭ�������Ф褤��
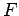 �θ�ͭ¿�༰
�θ�ͭ¿�༰ 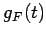 ��
��
 �θ�ͭ¿�༰
�θ�ͭ¿�༰ 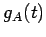 ����������
����������
�Ȥʤ롥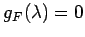 ����ͭ�ͤ�
����ͭ�ͤ�
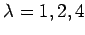 �Ǥ��롥
�Ǥ��롥
�Ȥʤ�Τǡ�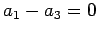 ,
,
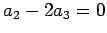 ��ꡤ
��ꡤ
 ��
�� 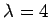 �˴ؤ����ͭ�٥��ȥ��
�˴ؤ����ͭ�٥��ȥ��
�������롥 ��ä�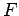 ��
�� 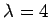 �˴ؤ����ͭ���֤�
�˴ؤ����ͭ���֤�
�Ȥʤ롥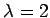 �ΤȤ���
�ΤȤ���
�Ȥʤ�Τǡ�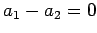 ,
, 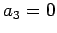 ��ꡤ
��ꡤ
 ��
�� 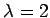 �˴ؤ����ͭ�٥��ȥ��
�˴ؤ����ͭ�٥��ȥ��
�������롥 ��ä�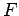 ��
�� 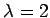 �˴ؤ����ͭ���֤�
�˴ؤ����ͭ���֤�
�Ȥʤ롥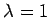 �ΤȤ���
�ΤȤ���
�Ȥʤ�Τǡ�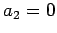 ,
, 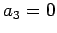 ��ꡤ
��ꡤ
 ��
�� 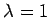 �˴ؤ����ͭ�٥��ȥ��
�˴ؤ����ͭ�٥��ȥ��
�������롥 ��ä�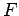 ��
�� 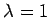 �˴ؤ����ͭ���֤�
�˴ؤ����ͭ���֤�
�Ȥʤ롥
��ɽ����롥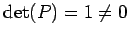 ���
���
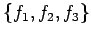 ��
1 ����Ω�Ȥʤ롥
��äơ�
��
1 ����Ω�Ȥʤ롥
��äơ�
�Ȥʤꡤ
������Ω�ġ�![$ \mathbb{R}[x]_2$](img410.png) ��
�� 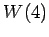 ,
, 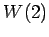 ,
, 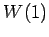 ��ľ��ʬ��롥
��ľ��ʬ��롥
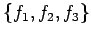 ��
��
![$ \mathbb{R}[x]_2$](img410.png) �δ���Ȥʤ롥
�δ���Ȥʤ롥
��ɽ����롥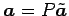 ��
��
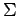 ����
���� 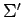 �ؤκ�ɸ�Ѵ��Ǥ��롥
�ؤκ�ɸ�Ѵ��Ǥ��롥
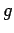 ��
�� 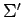 �ˤ������ɸ��
�ˤ������ɸ��
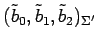 �Ȥ���ȡ�
Ʊ�ͤˤ���
�Ȥ���ȡ�
Ʊ�ͤˤ���
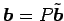 ������Ω�ġ�
�����Ѵ�
������Ω�ġ�
�����Ѵ� 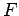 �������Ѵ�
�������Ѵ�
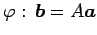 �������Ǥ��뤫�顤
�������Ǥ��뤫�顤
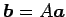 �˺�ɸ�Ѵ�
�˺�ɸ�Ѵ�
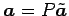 ,
,
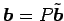 ����������
����������
�����롥 ����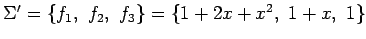 �˴ؤ���
�˴ؤ���
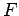 ��ɽ�������
��ɽ�������
�Ȥʤ롥
�θ�ͭ�͡���ͭ���֤���롥
�ޤ��������Ѵ� ![]() ��ɽ������
��ɽ������ ![]() ����롥
����
����롥
����
![]() �Τ�Ȥ�
¿�༰
�Τ�Ȥ�
¿�༰ ![]() ,
, ![]() �κ�ɸ��
�κ�ɸ��
![]() ,
,
![]() �Ȥ���ɽ���ȡ�
�Ȥ���ɽ���ȡ�
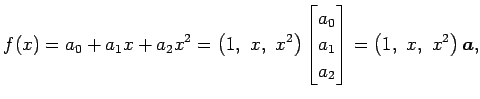 |
||
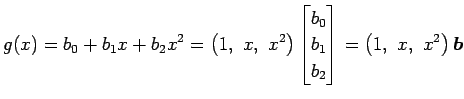 |
�Ƚ롥 ���ΤȤ���
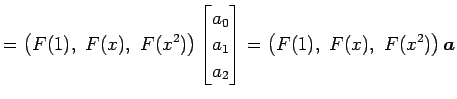 |
�Ȥʤ롥 ������
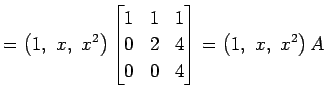 |
�Ǥ��뤫�顤���������
�������롥
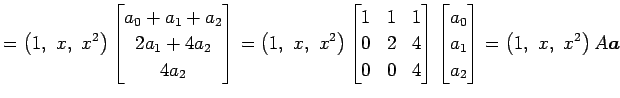 |
�Ȥ��Ƥ������롥 (��)��(��)��ꡤ �����Ѵ�
�ˤ���������������Ѵ�
���� ![]() �θ�ͭ�ͤ���롥
�θ�ͭ�ͤ���롥
![]() �˴ؤ����ͭ��������
�˴ؤ����ͭ��������
![]() �Ǥ��롥
(��)��(��)���Ѥ����
�Ǥ��롥
(��)��(��)���Ѥ����
��ɽ�����Τǡ� ��ͭ��������
�������Ǥ��롥 �Ĥޤ����
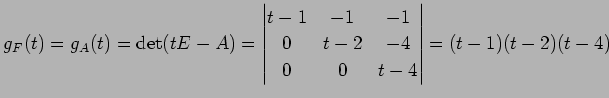 |
�Ȥʤ롥
![]() �θ�ͭ���֤���롥
��ͭ������(��)���
�θ�ͭ���֤���롥
��ͭ������(��)��� ![]() �θ�ͭ�٥��ȥ�
�θ�ͭ�٥��ȥ� ![]() ����ᡤ
���θ�(��)��������
����ᡤ
���θ�(��)�������� ![]() �θ�ͭ�٥��ȥ�
�θ�ͭ�٥��ȥ� ![]() ������Ф褤��
������Ф褤��
![]() �ΤȤ���
�ΤȤ���
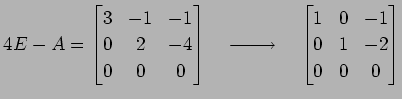 |
�Ȥʤ�Τǡ�
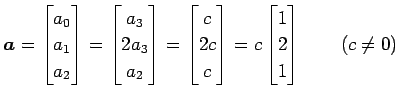 |
�������롥 ��ä�
�Ȥʤ롥
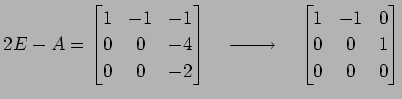 |
�Ȥʤ�Τǡ�
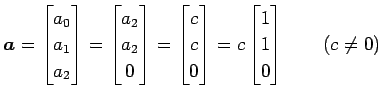 |
�������롥 ��ä�
�Ȥʤ롥
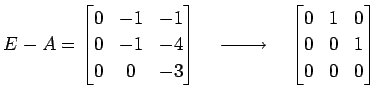 |
�Ȥʤ�Τǡ�
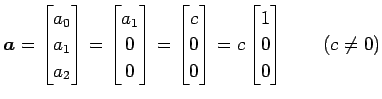 |
�������롥 ��ä�
�Ȥʤ롥
��ͭ���� ![]() ,
, ![]() ,
, ![]() �Τ��줾��δ����
�Τ��줾��δ����
![]() ,
, ![]() ,
, ![]() �Ǥ��롥
������
�Ǥ��롥
������
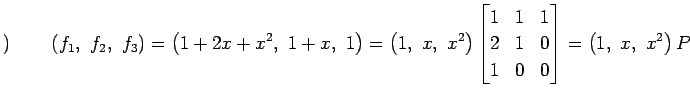 |
��ɽ����롥
�Ȥʤꡤ
������Ω�ġ�
�����Ѵ� ![]() �δ���
���
![]() �ˤ�����
ɽ�������
�ˤ�����
ɽ������� ![]() �Ǥ��롥
����
�Ǥ��롥
����
![]() �ˤ�����
�ˤ�����
![]() ��ɽ���������롥
����
��ɽ���������롥
���� ![]() �ˤ�����
�ˤ����� ![]() �κ�ɸ��
�κ�ɸ��
![]() �Ȥ���ȡ�
�����Ѵ�(��)���Ѥ��ơ�
�Ȥ���ȡ�
�����Ѵ�(��)���Ѥ��ơ�
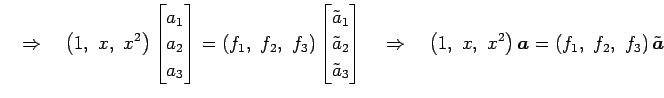 |
||
��ɽ����롥
�����롥 ����
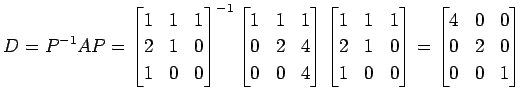 |
�Ȥʤ롥
���� 5.21 (���̤Υ٥��ȥ���֤θ�ͭ������)
���̤Υ٥��ȥ���֤ˤ������ͭ�������
���٥��ȥ����(
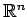 �ޤ���
�ޤ���
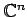 )�ˤ�����
��ͭ������˴Ը����Ƶ�������Ф褤��
�������Ǥϼ��Τ褦��Ʊ����Ԥä���
)�ˤ�����
��ͭ������˴Ը����Ƶ�������Ф褤��
�������Ǥϼ��Τ褦��Ʊ����Ԥä���
| �����Ѵ�
|
||
| �����Ѵ� |
||
| ��ͭ������
|
||
| ��ͭ����
|
���� 5.22 (���̤Υ٥��ȥ���֤ˤ����������Ѵ�)
�ɤΤ褦�ʥ٥��ȥ���֤ˤ�����
�����Ѵ��Ǥ��äƤ����  ��Ʊ��뤹��Ф褤��
��Ʊ��뤹��Ф褤��
Kondo Koichi

ʿ��18ǯ1��17��