5.7 一般の線形変換の固有値と固有空間
定義 5.17 (一般の線形変換の固有多項式)
ベクトル空間 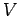 の基底を
の基底を
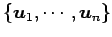 とする.
この基底における線形変換
とする.
この基底における線形変換 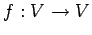 の表現行列を
の表現行列を  とする.
すなわち,
とする.
すなわち,
とする. このとき行列 の固有多項式
の固有多項式 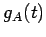 を
線形変換
を
線形変換  の固有多項式といい,
の固有多項式といい,
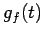 と表記する.
と表記する.
とする. このとき行列
定理 5.18 (一般の線形変換の固有多項式)
線形変換  の固有多項式
の固有多項式 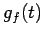 は
基底の取り方に依存しない.
は
基底の取り方に依存しない.
が成り立つ.これを用いて
を得る.
(証明)
基底を取り換えて表現行列が ![]() か
か ![]() にかわるととする.
このとき基底の変換行列を
にかわるととする.
このとき基底の変換行列を ![]() とすると
とすると
が成り立つ.これを用いて
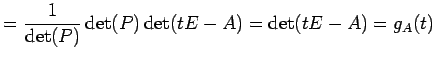 |
を得る.
定理 5.19 (一般の線形変換の固有値)
となる. よって の固有値と行列
の固有値と行列  の固有値は等しい.
の固有値は等しい.
(証明)
基底を
![]() とし,
固有値を
とし,
固有値を ![]() ,固有ベクトルを
,固有ベクトルを ![]() とする.
このとき
とする.
このとき
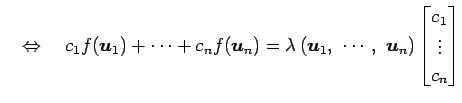 |
||
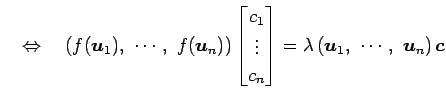 |
||
となる. よって
Kondo Koichi

平成18年1月17日