3.9 解をもつための連立 1 次方程式の条件
連立 1 次方程式
| (461) |
を考える. 以後この方程式に対して議論する.
方程式
![]() の解を求めるには
まず,拡大係数行列
の解を求めるには
まず,拡大係数行列
![]() の簡約化を行なう.
このとき得られた行列が
の簡約化を行なう.
このとき得られた行列が
![$\displaystyle [A\vert\vec{b}] \overset{\text{簡約化}}{\longrightarrow} \left[\b...
... & & &&& \cdots & 0 & 0 \\ 0 & \cdots & & &&& \cdots & 0 & 0 \end{array}\right]$](img954.png) |
(462) |
と得られたとしよう. このとき零ベクトルではない一番下の行に着目すると
| (463) |
となる.
![$\displaystyle A \overset{\text{簡約化}}{\longrightarrow} \left[\begin{array}{cc...
...& \cdots & & &&& \cdots & 0 \\ 0 & \cdots & & &&& \cdots & 0 \end{array}\right]$](img956.png) |
(464) |
であるから,
| (465) |
が成り立つ. この条件のもとでは解をもたない. 次に簡約化の結果として
![$\displaystyle = \left[\begin{array}{cccccccc\vert c} \!1\! & ** & \!0\! & ** & ...
... & & &&& \cdots & 0 & 0 \\ 0 & \cdots & & &&& \cdots & 0 & 0 \end{array}\right]$](img958.png) |
(466) |
を得たとする. こときは解をもつ. 係数行列のランクは
定理 3.33 (連立 1 次方程式の可解条件)
方程式
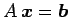 が解をもつための
必要十分条件は
が解をもつための
必要十分条件は
である.
| (467) |
である.
解に任意定数を含まないのは, 簡約行列のすべての列に主成分が現れるときである. つまり係数行列のランクと変数の個数が一致するときである. これをまとめると以下の定理を得る.
定理 3.34 (一意な解をもつ条件)
方程式
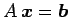 が唯一つの解をもつための
必用十分条件は
が唯一つの解をもつための
必用十分条件は
である.
| (468) |
である.
定理 3.35 (任意定数を含む解をもつ条件)
方程式
は
のとき任意定数を含む解をもつ. このとき任意定数の個数は
である.
| (469) |
は
| (470) |
のとき任意定数を含む解をもつ. このとき任意定数の個数は
| (471) |
である.
Kondo Koichi

平成17年9月15日