3.8 解が存在しない連立 1 次方程式
例 3.32 (解が存在しない具体例)
方程式
を考える. 拡大係数行列の簡約化を行なうと,
を得る. 方程式に書き戻すと
となる. 最後の行は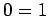 となるから,
どのような
となるから,
どのような 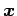 をとっても成立することはない.
よってこの連立方程式の解は存在しない.
ここで
をとっても成立することはない.
よってこの連立方程式の解は存在しない.
ここで
が成り立つことに注意する. このとき解をもたない.
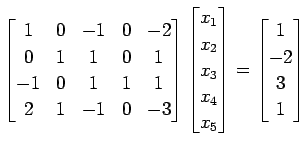 |
(457) |
を考える. 拡大係数行列の簡約化を行なうと,
![$\displaystyle = \left[ \begin{array}{ccccc\vert c} 1 & 0 & -1 & 0 & -2 & 1 \\ 0...
...0 \\ 0 & 0 & 0 & 1 & -1 & 0 \\ \hline 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right]$](img948.png) |
(458) |
を得る. 方程式に書き戻すと
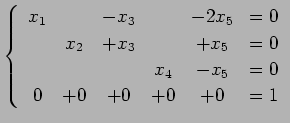 |
(459) |
となる. 最後の行は
| (460) |
が成り立つことに注意する. このとき解をもたない.
Kondo Koichi

平成17年9月15日