2.4 行列のいろいろ 〜 スカラー行列，上三角行列，下三角行列

定義 2.14 (スカラー行列)   対角成分の値がすべて等しい対角行列を スカラー行列（scalar matrix）と呼ぶ．

例 2.15 (スカラー行列の具体例)  

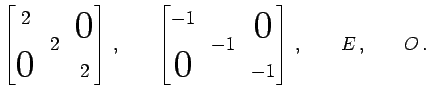$$\begin{bmatrix}2 & & \smash{\lower1.7ex\hbox{\text{\huge$0$}}}\\ ... ...-1 & \\ \smash{\text{\huge$0$}}& & -1 \\ \end{bmatrix}\,,\qquad E\,,\qquad O\,.$$ (267)

定義 2.16 (上三角行列)   対角成分を除く左下半分がすべて 0 の正方行列

$$A = \begin{bmatrix}a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ 0 ... ...\ddots & \vdots \\ \smash{\text{\huge$0$}}& & \cdots & 0 & a_{nn} \end{bmatrix}$$ (268)

を上三角行列（upper triangular matrix）と呼ぶ．

定義 2.17 (下三角行列)   対角成分を除く右上半分がすべて 0 の正方行列

$$A = \begin{bmatrix}a_{11} & 0 & & & \smash{\lower1.7ex\hbox{\text{\... ...\\ \vdots & & & \ddots & 0 \\ a_{n1} & a_{n2} & & \cdots & a_{nn} \end{bmatrix}$$ (269)

を下三角行列（lower triangular matrix）と呼ぶ．

Kondo Koichi
平成17年9月15日