2.5 転置行列
定義 2.18 (転置行列)
行と列の成分を入れ換えた行列
を転置行列(transposed matrix)と呼ぶ. 行と列を入れ換える演算を転置(transpose)をとるという. 転置された行列を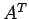 と書く.また
と書く.また 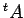 と書くこともある.
と書くこともある.
 |
(270) |
を転置行列(transposed matrix)と呼ぶ. 行と列を入れ換える演算を転置(transpose)をとるという. 転置された行列を
例 2.19 (転置の具体例)
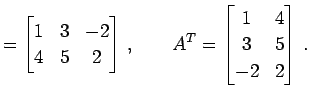 |
(271) |
問 2.20
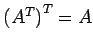 を示せ.
を示せ.
となる.証明終了.
(証明)
![]() ,
,
![]() とおく.
行と列を入れ換えるので
とおく.
行と列を入れ換えるので ![]() は
は
![]() とも書ける.
つまり
とも書ける.
つまり
![]() となる.
転置をとる操作を成分でみると,
行と列の添字を入れ換える操作に対応する.
よって
となる.
転置をとる操作を成分でみると,
行と列の添字を入れ換える操作に対応する.
よって
![$\displaystyle = {({[a_{ij}]}^{T})}^{T}= {([a_{ji}])}^{T}= [a_{ij}]=A$](img628.png) |
(272) |
となる.証明終了.
Kondo Koichi

平成17年9月15日